Kugelflächenfunktionen

Eine stehende Welle um eine Kugel lässt sich als stationärer Zustand interpretieren. Damit ist jeder Zustand einer Welle räumlich fixiert. Die Frage ist nun: wie viele Wellen passen auf bzw. um eine Kugel?

In der klassischen Mechanik versteht man unter Freiheitsgrad die Zahl der frei wählbaren, voneinander unabhängigen Bewegungsmöglichkeiten eines Systems.
Ein starrer Körper im Raum hat den Freiheitsgrad f = 6, denn man kann den Körper in drei voneinander unabhängige Richtungen bewegen und in drei voneinander unabhängigen Ebenen drehen.

Da eine Kugel rotationssymmetrisch ist, spielen Drehungen keine Rolle. Eine Kugel besitzt demnach 3 Freiheiten bezüglich einer Wellenausbreitung. Daher sind drei unabhängige Wellen um die Kugel herum möglich.
Durch die Kugelgestalt bedingt lassen sich die drei Freiheiten auch als Kugelkoordinaten darstellen.

Beispiel Erde:

1) Eine Schwingung läuft von Nordpol über Südpol wieder zum Nordpol
2) Die zweite Schwingung läuft um den Äquator herum
3) Die dritte stehende Welle verläuft radial – vom Mittelpunkt ausgehend

Für die ersten beiden Beispiele existiert ein mathematisches Konzept, dass sich hier für eine Darstellung eignet, nämlich die Kugelflächenfunktionen.

Stehende Wellen auf einer Kugeloberfläche können als Kugelflächenfunktionen behandelt werden.

Es existieren 3 Arten:

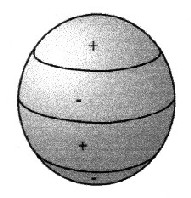		Zonale Kugelflächenfunktionen hängen lediglich vom Breitengrad ab sin φ cos φ
Abbildung 2.1.1 - zonale Kugelflächenfunktionen

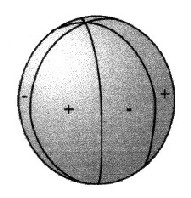		Sektorielle Kugelflächenfunktionen hängen lediglich vom Längengrad ab sin λ cos λ
Abbildung 2.1.2 - sektorielle Kugelflächenfunktionen

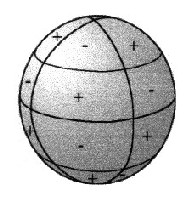		Tesserale Kugelflächenfunktionen hängen vom Breitengrad und vom Längengrad ab sinφ·sinλ sinφ·cosλ cosφ·sinλ cosφ·cosλ
Abbildung 2.1.3 - tesserale Kugelflächenfunktionen

Erläuterung:

Ein komplettes streckenmassig quadratisches Gitter auf einer Kugel lässt sich nicht verwirklichen.

Es entstehen lediglich Gittersysteme, die wie das geographische Gittersystem gestaltet sind. Es existieren immer zwei Pole. Die zugehörigen „Meridiane“ und „Breitenkreise“ bilden dann das Gitter.

bei Amazon kaufen

284 Seiten, davon 44 in Farbe
220 Bilder
57 Tabellen

Herstellung und Verlag:
Books on Demand GmbH, Norderstedt

ISBN 978-3-7494-8112-5

Ladenpreis: 17,50 Euro

	Copyright © Klaus Piontzik


Englische Version

2.1 - Kugelflächenfunktionen

Zonale Kugelflächenfunktionen

Sektorielle Kugelflächenfunktionen

Tesserale Kugelflächenfunktionen