| Copyright © Klaus Piontzik | ||
| Englische Version |
| Zu bestimmen ist also der Mittelpunktabstand MA = l’ einer magnetischen Schicht. |
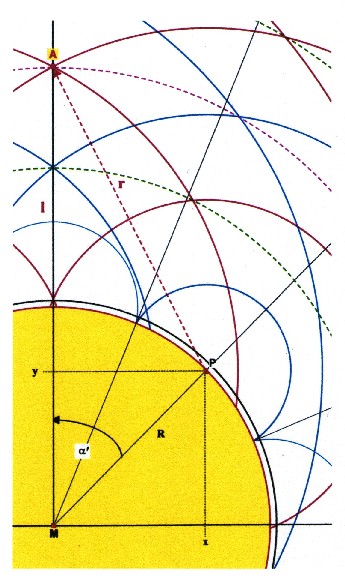 |
| Abbildung 2.5.2.1 – Distanzberechnung der magnetischen Schichten |
| Für die Strecke MA gilt: |
| und |
| Es gelten die Beziehungen: |
| Der Radius der Kugel R Beruhend auf Kapitel 2 lässt sich jeder Schwingung ein bestimmter Winkel α zuordnen: |
| Für den Grundwinkel gilt: |  |
| n ist die Anzahl
der Schwingungen um den Umfang herum. Alternativ wäre
hier auch die Anwendung von Gleichung 2.05 möglich. Der Abstand von einem Quellpunkt des Feldes zum nächsten beträgt die Hälfte des Winkels Alpha. Berücksichtigt man alle Quellpunkte, so treten diese in ganzzahligen Vielfachen des halben Grundwinkels auf. Es gilt also: |
| Vielfache des Winkels: | 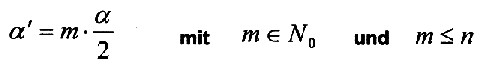 |
| In der nebenstehenden Abbildung
gilt für den Quellpunkt P: m = 2 Die Strecke PA = r entspricht dem Weg, den die Welle zurücklegt. Vom Quellpunkt P ausgehend, bis zu der Schwingungsschicht (Punkt A), die zu bestimmen ist. Durch den stationären Zustand bedingt, entstehen Maximal- und Minimalfronten, die sich kugelförmig um den Quellpunkt, in regelmäßigen Abständen ausbilden. Nach Kapitel 2 entspricht jeweils ein Abstand der halben Wellenlänge. Daher ist der Weg der Welle bis zur Schwingungsschicht stets ein ganzzahliges Vielfaches der halben Wellenlänge: |
| Die von der Welle zurückgelegte Strecke: |  |
| In Abbildung 2.5.2.1 gilt für den Wellenweg PA: k = 4 |
| Für die Wellenlänge gilt: | 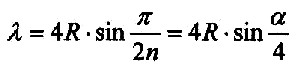 |
| Einsetzen aller behandelten Terme in die Gleichung für l’ führt zu folgendem Ergebnis: |
| 2.5.2.1 - Gleichung: | 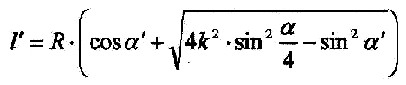 |
| Werden Alpha und Alpha strich noch durch die entsprechenden Terme aus den vorherigen Betrachtungen ersetzt, so entsteht die folgende Schichtengleichung: |
| 2.5.2.2 - Gleichung: | 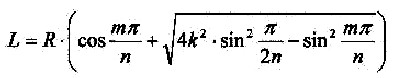 |
n,m,k = 1,2,3,4,... |
| R = Radius der
Kugel n = Anzahl der Schwingungen m = Anzahl der Quellen – aus Symmetriegründen 1 ≤ m ≤ n k = Anzahl der halben Grundwellenlänge um eine Schicht zu erreichen n, m, k sind ganzzahlige Parameter die, bei sukzezziver Anwendung, eine Tabelle von Schichten L liefern |
| 2.5.2.3 - Satz: | Mit dem Radius R der Kugel sind auch alle möglichen Schichten L gegeben. |
| 2.5.2.4 - Definition: Es ergibt sich diese vereinfachte Sicht des resultierenden Feldes: |
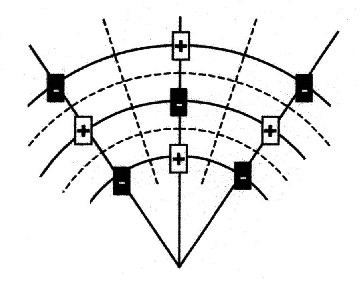 |
| Abbildung 2.5.2.2 – Gitterbildung |
| Durchgezogene Linien =
Extremal-Linien = Pol-Schichten Gestrichelte Linien = Null-Linien = Nullwände |
| Es existieren zwei Betrachtungsmöglichkeiten: |
| 2.5.2.5 - Satz: | Die Pole
bilden ein gitterförmiges radiales
Schichtensystem. Die Polschichten sind stationäre Extremalzustände. Betrachtet man zwei direkt übereinander liegende Polschichten, so besitzen diese Schichten stets eine gegenphasige Ordnung der Pole zueinander. |
| 2.5.2.6 - Satz: | Die Nullwände
bilden ein gitterförmiges radiales
Schichtensystem. Die Pole liegen im Mittelpunkt des jeweils einhüllenden Null-Feldes. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |