| Copyright © Klaus Piontzik | ||
| Englische Version |
| Ziel
dieses Kapitels ist es eine Beschreibung von
mathematischen und physikalischen Grundbedingungen zu
liefern, die der Entwicklung einer Gleichung für ein
Schwingungsgefüge dienen und damit eine Quantifizierung
des Modells erlauben. Der Ansatz erfolgt auf der Basis
von Schwingungen auf bzw. um eine Kugel herum. Beispiele für Schwingungsmöglichkeiten: |
|
|
|
| Sinus | Kosinus | - Kosinus |
Abbildung
2.0.1 Schwingungen
Sinus bzw. Kosinus = Schwingung = Welle
Für physikalische Schwingungen gilt:
Wie erhält man Schwingungen um eine Kugel herum? - Analog zum Bohrschen Atommodell, d.h. wenn man nach De Broglie das umlaufende Elektron als Welle auffasst: |
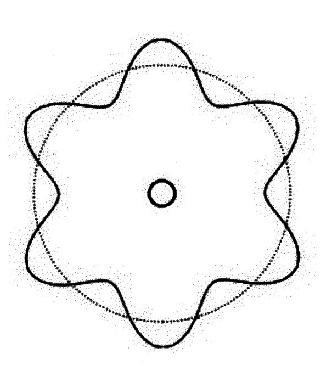
Abbildung 2.0.2 Schwingungen um eine Kugel
Es passt nur eine ganzzahlige Anzahl von Schwingungen um die Kugel.
Die Wellenlänge Lambda ist proportional zum Kreiswinkel Alpha:
|
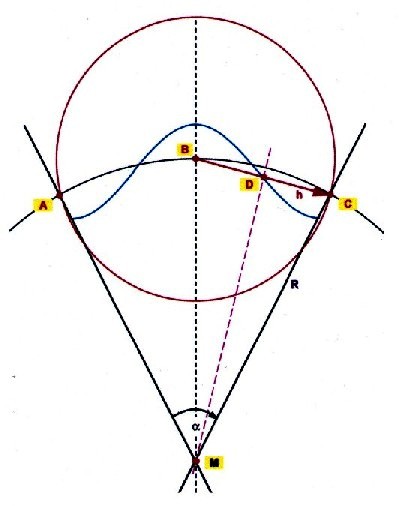
Abbildung 2.0.3 Wellenlänge und Kreiswinkel
Bedingung für n Schwingungen um eine Kugel:
Hier schließt sich der Schwingungskreis nicht schon nach einer Umdrehung sondern erst mach m Umdrehungen. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |