| Copyright © Klaus Piontzik | ||
| Englische Version |
| Allgemein lassen sich 11 relevante atmosphärische Schichten zusammen tragen. Hierbei werden die einzelnen Schichten nach Höhe geordnet und durchnummeriert. |
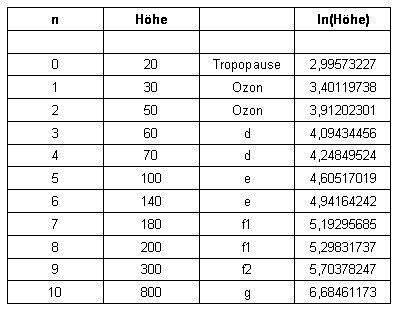
| Rechts in der Tabelle befindet
sich der Logarithmus naturalis für die
jeweiligen Höhen. Der Logarithmus der Höhe wird als Funktion einer Nummerierung dargestellt: |
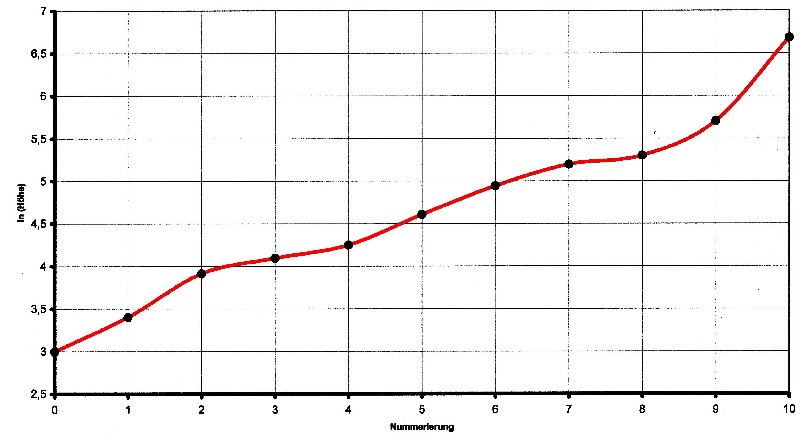
| Abbildung 3.8.1 – Logarithmus der Höhe |
| Die Funktion in Abbildung 3.8.1
sieht, bis auf Teilstücke, zuerst mal nicht sehr linear
aus. Schaut man sich den Verlauf aber näher an so
erkennt man: a) Zwischen Punkt 2 bis 7 ist die Steigung anähernd konstant. b) Zwischen Punkt 1 und 2 sowie zwischen Punkt 8 und 9 ist die Steigung so groß, dass dort noch ein Punkt eingeschoben werden kann um die Steigung abzuflachen. c) Zwischen Punkt 9 und 10 die Steigung so groß, dass dort noch mehrere Punkte eingeschoben werden können. Daher entfällt Punkt 10 erst mal. d) Zwischen Punkt 7 und Punkt 8 ist die Steigung so klein, dass dort die Nummerierung auf ein halb gesetzt werden kann, um so die Steigung zu erhöhen. Die in der Nummerierung korrigierten Schichten nach Höhe geordnet, ergeben dann die folgenden Tabelle: |
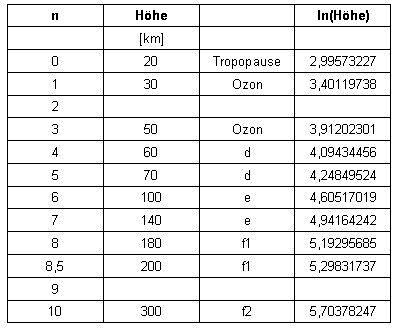
| Deutlich sind in der Tabelle die neu hinzugekommenen Schichten bei den Nummerierungen 2 und 9 zu erkennen. Die korrigierte Funktion sieht dann so aus: |
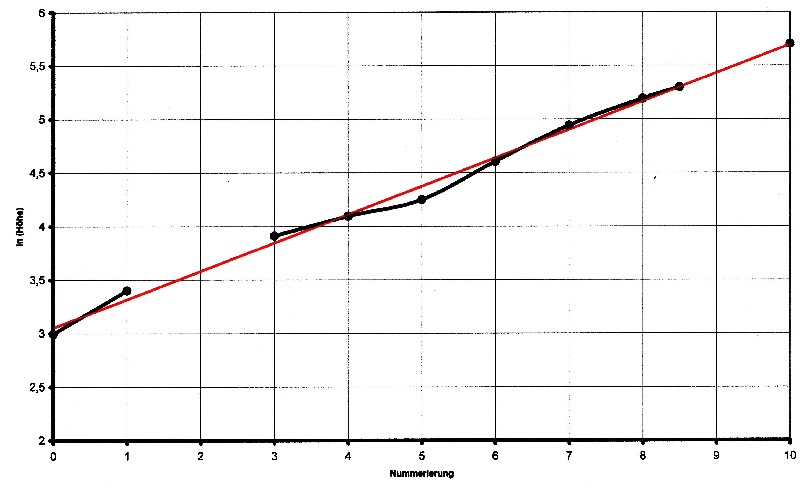
| Abbildung 3.8.2 – Linearisierung |
| Die rote Linie in Abbildung 3.8.2
stellt eine Gerade dar, die durch lineare Regression aus
der korrigierten Tabelle ermittelt wurde. Wie zu sehen ist, stimmen die Schichtenwerte jetzt gut mit der Näherungsgeraden überein. Für die Näherungsgerade lassen sich die folgenden Werte ermitteln. Es gilt für die additative Konstante: b = ln wMin = ln H0 = ln 20 = 2,995732 Es gilt für die Steigung der Geraden: Δ y = ln wMax – ln wMin = ln 320 – ln 20 = 2,772588 Δ x = n = 10 a = Δ y/Δ x = 2,772588/10 = 0,277258 Es kann hier also eine lineare Funktion für die atmosphärischen Schichten, als Lösungsansatz, benutzt werden. Allgemein gilt für die Gerade aus Abbildung 3.8.2: y = ln(Höhe) = a·x + b Die gefundenen Werte werden in die Geradengleichung eingesetzt : |
| Es ergibt sich: | ln(Höhe) = 0,277 · x + 2,9957 |
| Durch Umstellen erhält man: |
| 3.8.1 - Gleichung: | Höhe = 20 · e0,277·x [Km] |
| Setzt man x = n so ergibt sich für Gleichung 3.8.1 folgender Funktionsverlauf: |
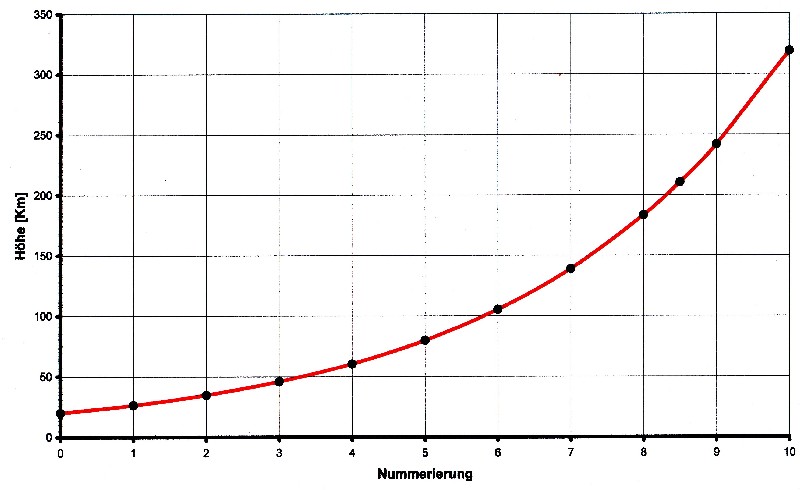
| Abbildung 3.8.3 – Höhe als e-Funktion |
| Gleichung 3.8.1 besitzt alle
Eigenschaften die nach 2.11.3 notwendig sind, um als
Lösungsfunktion der Laplace-Gleichung in Betracht zu
kommen. Damit stellen die atmosphärischen Schichten eine Lösung der Laplace-Gleichung, speziell des Radialanteils, dar. In der Konsequenz lässt sich folgender Satz aufstellen: |
| 3.8.2 - Satz: | Die atmosphärischen Schichten sind Ausdruck eines Schwingungsphänomens. |
| Es lassen sich an der
Gleichung noch Vereinfachungen vornehmen. Es gilt: 0,277 = 3,6-1 = 5/18 Sämtliche Werte eingesetzt ergibt: |
| 3.8.2 - Gleichung: | 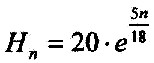 |
[Km] |
| Es kann folgende Beziehung
aufgestellt werden (siehe Satz 5.1.5): rik = RE/5 · rik = innerer Kern und RE = 6371 Km und es gilt weiterhin: 5100 = RE– rik = 4/5 · RE = 4rik 5100 = 255 · 20 ==> 20 = 4/255·rik Dann lässt sich für die atmosphärischen Schichten schreiben: |
| 3.8.3 - Gleichung: | 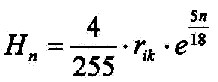 |
[Km] |
| Dann lässt sich weiterhin für die atmosphärischen Schichten schreiben: |
| 3.8.4 - Gleichung: | 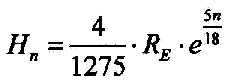 |
[Km] |
| Die Schichten nach Höhe geordnet und die errechneten Werte ergeben die folgende Tabelle: |
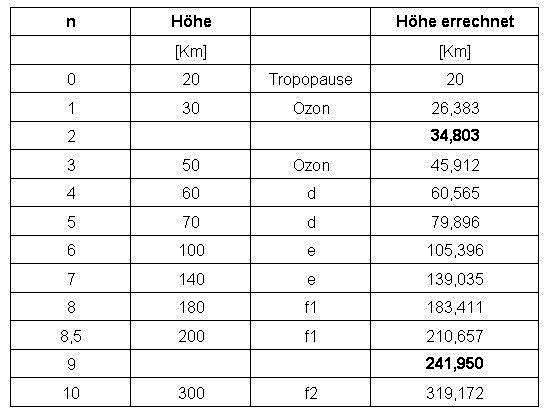
| Der mittlere Fehler der
errechneten Werte für die Schichten liegt unter
2 Prozent.. Zusätzlich entstehen noch einmal zwei Schichten. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |