| Copyright © Klaus Piontzik | ||
| Englische Version |
| Schon C.F.
Gauß und W. Weber erkannten 1838,
durch ihre Versuche mit dem Erdmagnetfeld, dass das
Magnetfeld nicht einfach durch das Modell eines
Stabmagneten bzw. einer Leiterschleife erklärt werden
kann. 1838 erschien die „Allgemeine Theorie des Erdmagnetismus“ von C.F. Gauß und W. Weber in der sie folgende Potentialgleichung für das Erdmagnetfeld angeben: 4.1.1 - Gleichung: |
|
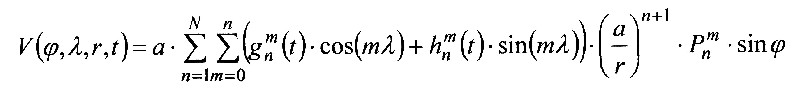 |
|
|
|
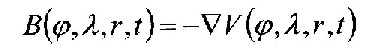 |
| Nach Gleichung 4.1.2 ist die magnetische Flussdichte B abhängig vom Breitengrad φ, vom Längengrad λ, Abstand r vom Mittelpunkt und der Zeit t. |
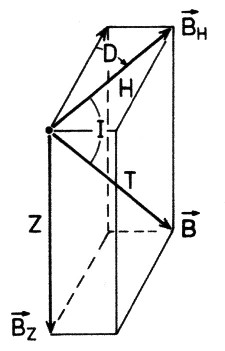 |
Aus diesem Vektor
lassen sich die sogenannten Feldelemente des
Magnetfeldes generieren. Also, die Deklination, die Inklination und die Totalintensität usw. |
| Abbildung 4.1.1 – Feldelemente |
| Die Gleichungen von Gauß und
Weber für das Erdmagnetfeld werden bis heute benutzt. Aus der Potentialgleichung bzw. der Theorie lassen sich aber die real auftretenden Koeffizienten in der Potentialgleichung nicht ermitteln. Dies geschieht über eine Messung des realen magnetischen Feldes der Erde. Bemerkung: Löst man die Klammern in der Potentialgleichung auf, so treten in der Gleichung von Gauß lediglich Produkte von Sinus- bzw. Kosinus-Funktionen, also tesserale Kugelflächenfunktionen bzw. Gitter auf. Das heißt: Schon Gauß und Weber legten bei ihren Betrachtungen des Erdmagnetfeldes Kugelflächenfunktionen zugrunde!!! Siehe dazu auch „Gitterstrukturen des Erdmagnetfeldes“, Kapitel 2.7, Der Ansatz von Gauß, Seite 32–33. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |