| Copyright © Klaus Piontzik | ||
| Englische Version |
| Um Magnetfelder messen zu können, bedarf es eines physikalischen Effektes,
der auf magnetische Flussdichte B reagiert. Solch ein Phänomen liefert der Hall-Effekt. |
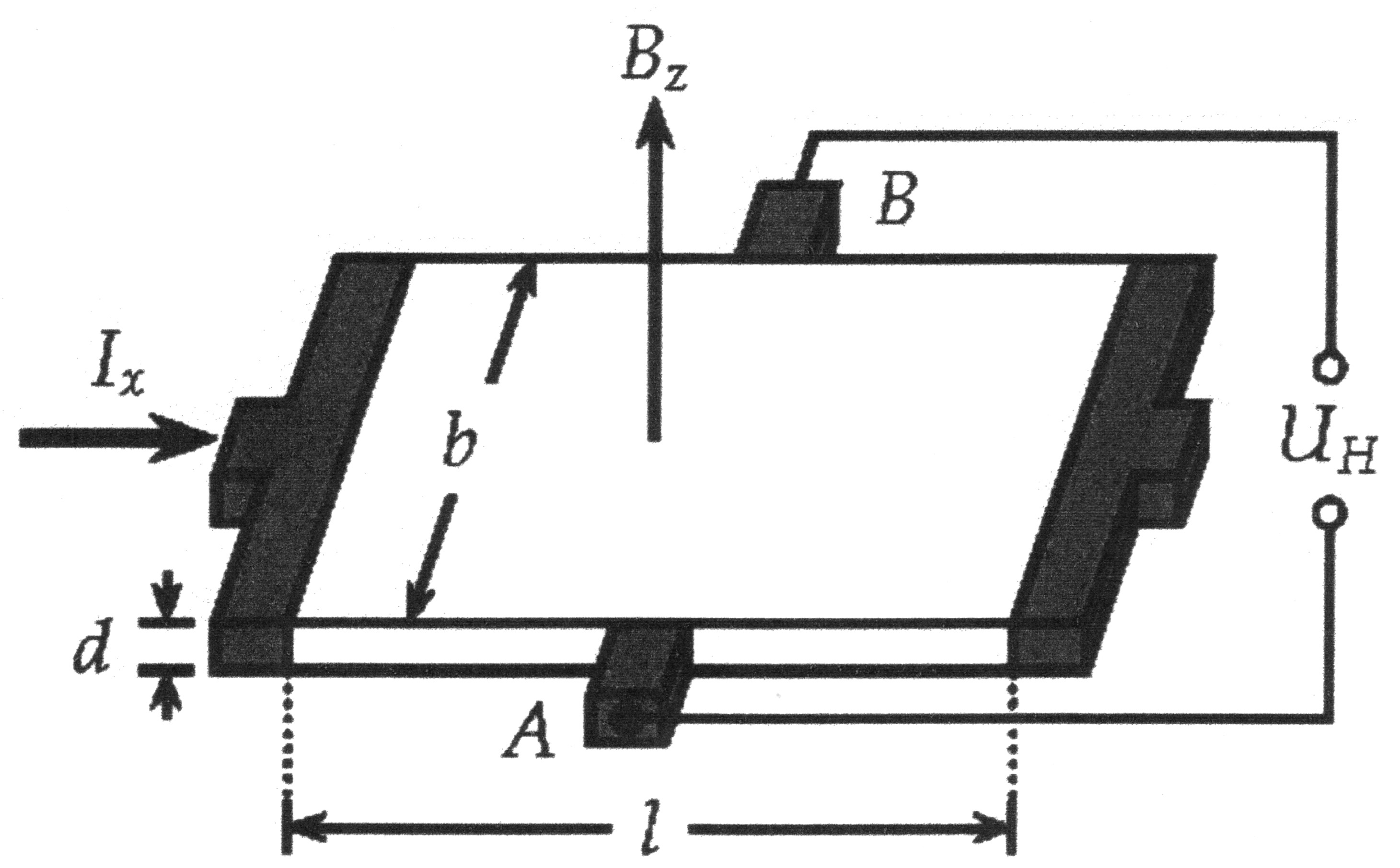 |
| Abbildung 6.1.1 – Hallsensor |
| Wie in der Abbildung 6.1.1 dargestellt, wird eine sehr dünne Metallplatte
von einem gleichmäßig über ihren Querschnitt verteilten Strom Ix durchflossen. Zwischen zwei Punkten
A und B, die gleich weit von den Stromzuleitungen entfernt liegen und die mit einem Galvanometer verbunden sind,
ist keine Spannung feststellbar.
Wird das Plättchen von einem Magnetfeld B durchsetzt, so wirkt auf die bewegten Ladungsträger des primären Stromes I die Lorentz-Kraft F. Diese Kraft hebt die gleichmäßige Ladungsverteilung im Plättchen auf und führt zu einer Potentialdifferenz UH zwischen den zwei Punkten A und B. Es fließt ein Strom durch einen an diesen Punkten angeschlossenes Galvanometer. Die durch die Lorentz-Kraft bewirkte Ladungsverteilung erzeugt ein elektrisches Feld mit der Feldstärke E, das der Ablenkung der Ladungsträger entgegenwirkt. Es stellt sich ein Zustand ein, bei dem die Lorentz-Kraft FL und die vom elektrischen Feld bewirkte Gegenkraft FE den gleichen Betrag haben. Aus diesen Randbedingungen lässt sich die allgemeine Gleichung für die Hallspannung ableiten: |
| 6.1.1 Gleichung |
| Wobei RH der Hallkoeffizient, sowie d die Materialdicke des Metallplättchen
als spezifische Konstanten eines Hallsensors zu betrachten sind, die in einer Konstanten k zusammengefasst werden.
Dann lässt sich allgemein schreiben: |
| 6.1.2 Gleichung |
| Die Hallspannung ist nur vom Speisestrom IB des Sensors und der Flussdichte B
des einwirkenden magnetischen Feldes abhängig. Wobei der Hallsensor mit einer Gleichspannung betrieben
wird, d.h., I ist konstant. In dieser Konfiguration wird der Hallsensor normalerweise als magnetisches Flussdichtemessgerät verwendet. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |