| Copyright © Klaus Piontzik | ||
| Englische Version |
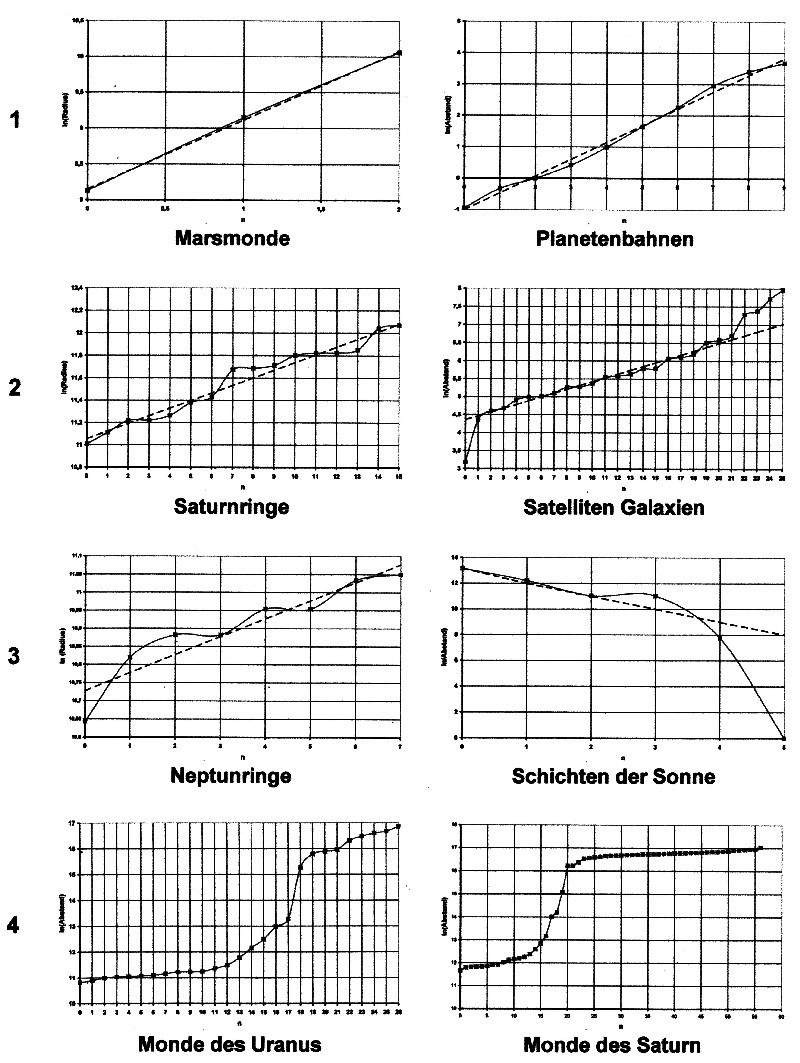
| Die gegebenen Werte wk werden (in einem nächsten Schritt) logarithmiert. Die logarithmierten Werte werden als Funktion der Nummerierung dargestellt. Siehe dazu die Bilder aus Abbildung 7.1. |
| Abbildung 7.1 Logarithmierte Werte |
| Nach der
Logarithmierung muss zumindest ein annähernd lineares
Verhalten der Funktion vorhanden sein. Diese Linearität ist notwendige Voraussetzung dafür, dass sich die Folge von n Werten auch in eine e-Funktion umwandeln lässt. Bei zwei Werten kann der zweite Wert auf eine beliebige Nummerierungsposition geschoben werden. Damit ist keine eindeutige Gerade definierbar. Erst wenn mindestens drei Werte vorhanden sind, lässt sich daraus eine eindeutige Gerade extrahieren. Die Bilder aus Abbildung 7.1 zeigen die verschiedenen Formen von Funktionen, wie sie real bei der Logarithmierung auftreten können. Zeile 1An den
Bildern zu den Marsmonden und den Planetenbahnen ist eine
fast perfekte Linearität der logarithmierten Werte zu
erkennen. Zeile 2Am Bild der Saturnringe ist eine gute Linearität der logarithmierten Werte zu erkennen. Am Bild der Satellitengalaxien ist zu
erkennen, dass die meisten Daten schon eine gute
Linearität besitzen. Lediglich im Nahbereich und im
Fernbereich sind abweichend Werte vorhanden, die dann,
durch die noch folgende Linearisierung, geglättet werden
können. Zeile 3Am Bild zu den Neptunringen ist eine gute Linearität der logarithmierten Werte zu erkennen. Die
Schalen der Sonne sehen auf den ersten Blick nicht linear
aus. Man sollte aber beachten, dass Punkt 3 hier etwa auf
gleicher Höhe wie Punkt 2 liegt, was einen ganzen
Zählschritt nicht rechtfertigt. Wenn Punkt 4 nach 5
versetzt wird, ergibt sich schon eine erstaunlich gute
Linearität. Dies zeigt, dass über eine genäherte
Nummerierung eine größere Linearität zu erreicht
werden kann. ZwischenbilanzDie
Linearität der logarithmierten Werte ist bei den
Beispielen aus den Zeilen 1, 2 und 3 schon so gut, dass
hier von einem starken Zusammenhang zur e-Funktion
ausgegangen werden kann. Zeile 4Bei den Monden des Uranus ist deutlich die treppenartige Struktur zu erken-nen. Der steile Anstieg zwischen den Punkten 17 und 18 bedeutet nichts anderes als die Existenz eines großen Freiraumes zwischen den Bahnen. Bei allen Planeten lassen sich die Bahnen der Monde in zwei Teilbereiche aufspalten. In einen Nahbereich und in einen Fernbereich. Trennt man die beiden Bereiche und behandelt sie getrennt, so lässt sich auch hier eine gute Linearisierung erreichen. Bei den Monden des Uranus ist ebenfalls deutlich die treppenartige Struktur zu erkennen. Auch hier ergeben sich wie bei Uranus ein Nah- und ein Fernbereich. Im Unterschied zu Uranus existieren aber auch Monde im Bereich der Lücke, so dass hier von einem Mittelbereich gesprochen werden kann. Tauchen Diagramme wie bei den Monden des Saturn und Uranus auf, so werden erst mal nur die Daten aus dem Nahbereich verwertet. Der Mittel- bzw. Fernbereich wird dann durch Extrapolation der gefundenen Funktion gewonnen. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |