| Copyright © Klaus Piontzik | ||
| Englische Version |
Es
existieren zwei Möglichkeiten um aus den logarithmierten
(und linearisierten) Daten eine Näherungsgerade
zu ermitteln.
Im folgenden wird hier Fall b) behandelt, da Fall a) über ein handelsübliches Kalkulationsprogramm behandelt werden kann. Gesucht wird nun die Näherungsgerade y = ax + b für die logarithmierten Werte. In der folgenden Abbildung ist die Näherungsgerade als gestrichelte Linie eingezeichnet. |
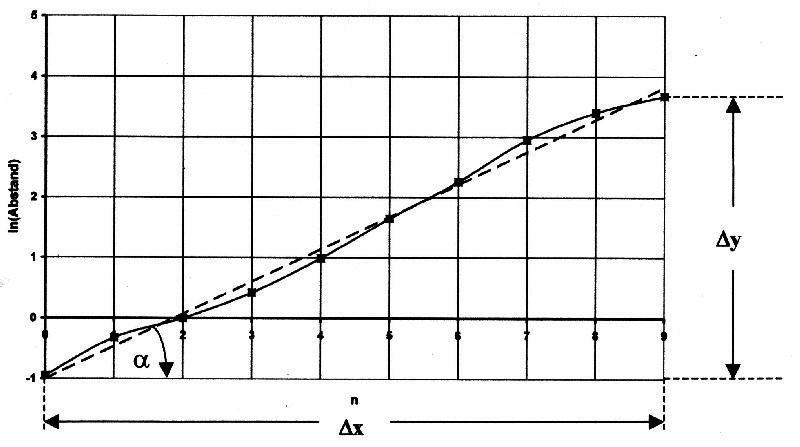
Abbildung 7.2 Näherungsgerade
Es sind n Werte gegeben, nämlich: y0, y1, y2, ... yk, ... yn
mit yk = ln wk
Es existiert ein Minimum ymin und ein Maximum ymax
| Die Steigung a der Näherungsgeraden lässt sich aus den Min-Max-Werten und der neuen genäherten Nummerierung ermitteln. Es gilt: |
| 7.4.1 - Gleichung: |
|
| delta y ist die Differenz zwischen Minimal- und Maximalwert: |
| 7.4.2 - Gleichung: |
|
| delta x ist der Maximalwert der neuen Nummerierung: |
| 7.4.3 - Gleichung: |
|
| Die additative Konstante der gesuchten Funktion ergibt sich aus dem kleinsten Wert: |
| 7.4.4 - Gleichung: |
|
| Für die Näherungsgerade gilt: |
| 7.4.5 - Gleichung: |
|
| Einsetzen aller Terme ergibt: |
| 7.4.6 - Gleichung: |
|

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |