| Copyright © Klaus Piontzik | ||
| Englische Version |
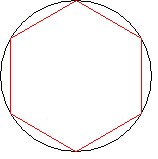 |
Die Eckpunkte der
Polyeder liegen auf der umhüllenden Kugel.Alle
Kanten werden auf die Kugeloberfläche übertragen. Im Unterschied zu allen anderen planetaren Systemen treten hier, durch die Polyederstruktur bedingt, erstmal Linien mit endlichen Längen auf. |
| Abbildung 1.2.4 – Polyeder im Querschnitt |
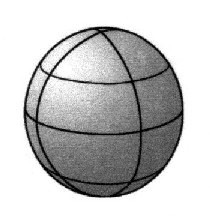 |
Die Kanten bzw. Ecken
der Polyeder kann man also auf die umhüllende Kugel
projizieren. Die beste Methode besteht darin alle Ecken eines Polyeder, wie beim geografischen System, als Schnittpunkte von Breitenkreisen und Meridianen abzubilden. |
| Abbildung 1.2.5 – Gitterbildung |
| Die Kreuzungspunkte des so
entstandenen Gitters entsprechen den Ecken des Polyeder.
Und die Kanten des Polyeder liegen in der Regel auf den
Breitenkreisen bzw. Meridianen. Der Oktaeder ist der einzigste platonische Körper bei dem alle Polyederkanten und Gitterlinien komplett überein stimmen. Das Gitter wird durch drei, jeweils senkrecht aufeinander stehende, Kreise gebildet. Dadurch wird die Kugeloberfläche in acht gleiche Teile zerlegt. Der Kubus besitzt eine Zerlegung die durch vier Kreise gebildet wird und ebenfalls ein symmetrisches Gitter bildet. Alle waagerechten Kanten des Kubus sind mit den Breitenkreisen identisch. Alle senkrechten Kanten des Kubus sind in den Meridianen als Teile enthalten. Der Tetraeder besitzt einerseits die gleiche Zerlegung wie der Kubus, da ein Tetraeder als Innenkörper eines Kubus dargestellt werden kann. Es treten dann aber Kanten am Polyeder auf, die im Koordinatensystem nicht direkt abgebildet werden. Eine andere Möglichkeit beim Tetraeder besteht darin diesen als dreieckige Pyramide zu sehen. So erhielte man drei Meridiane und einen Breitenkreis, aber dadurch auch ein unregelmäßiges Gitter. Auch der Ikosaeder liefert ein regelmäßiges Gitter mit fünf Meridianen und zwei Breitenkreisen. Es treten aber Kanten am Polyeder auf, die im Koordinatensystem nicht direkt abgebildet werden . Lediglich der Pentagon-Dodekaeder bildet mit fünf Meridianen und vier Breitenkreisen in den Distanzen der Breitenkreise zueinander unregelmäßige Abstände aus. Insgesamt lässt sich so folgende Aussage formulieren: |
| 1.2.2 - Satz: | Polyeder
<=> Gitter Polyeder sind äquivalent zu Gittern auf einer Kugeloberfläche. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |