| Copyright © Klaus Piontzik | ||
| Englische Version |
| 1952 wollte der
deutsche Physiker W. O. Schumann, von
der Technischen Universität München, seinen Studenten
Übungsaufgaben zur Elektrizitätslehre stellen. Thema
war damals die Berechnung von Hohlraumresonatoren.
Dabei gab er vor, dass die Unterseite der Ionosphäre, also die Heavisideschicht, die eine Kugel und die Erdoberfläche die andere Kugel des Resonators sein sollte. Die Aufgabe bestand darin, die Eigenfrequenz (Resonanz) dieses Hohlraumresonators zu ermitteln. Als Ergebnis erhielt er 7,8 Hz. Diese Aufgabe lässt sich nur mittels der Differential- bzw. Integralrechnung lösen. Die Lösung erfolgt über die Ermittlung sogenannter transversal-magnetischer Wellen (TM-Wellen) in einem Hohlraumresonator. Diese werden heute als Schumannwellen oder auch Schumann-Resonanzen bezeichnet. Die Schumann-Frequenz ist die Eigenfrequenz des Erdoberflächen-Ionosphären-Hohlraumresonators. Die Konsequenz ist: |
| 3.11.1 - Satz: | Die Schumann-Frequenz ist die Eigenfrequenz der Atmosphäre. |
| 3.11.2 - Definition: | Schumannfrequenz = fS = 7,83 Hz |
| Aus den Gleichungen 2.4.3 und 3.10.1 lassen sich zwei einfache Relationen der Erdfrequenz und der Schumann-Frequenz zur Grundhülle L0 ableiten: |
| 3.11.3 - Gleichungen: | 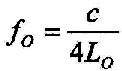 |
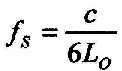 |
| Es existiert noch folgender Zusammenhang zu den Sferics: |
| Sferic-Grundfrequenz: | 4150,84 Hz = 11 · 25 · fo und fo = 3/2 fS |
| Es gilt daher auch: |
| Sferic-Grundfrequenz: | 4150,84 Hz =
33 · 24 · fS 33. Eigenschwingung = 32. Oberwelle |
| 3.11.3 - Satz: | Die Sferic-Grundfrequenz ist die 4. Oktave der 32. Oberwelle der Schumannfrequenz. |
| Ergänzende Informationen sind in dem Buch „Gitterstrukturen des Erdmagnetfeldes“ Kapitel 15, Magnetische Schichten und Frequenzen 1, Seite 129, zu finden. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |