| Copyright © Klaus Piontzik | ||
| Englische Version |
|
Aus der Schule, und aus den Me-dien, kennen
wir das Magnetfeld der Erde stets als ein Feld, dass dem
Feld eines Stabmagneten entspricht. Es ist das sogenannte
Dipolfeld. Historisch bedingt erklärt diese Sichtweise des Magnetfeldes das Verhalten einer Inklinationsnadel. Die Nadel steht am Pol senkrecht zur Erdoberfläche und am Äquator waagerecht zur Erdoberfläche. |
|
| Abbildung 4.0.1 – Dipolfeld |
| Nimmt man gemessene Werte des Feldes, so lässt sich an den auftretenden vier magnetischen Polen (siehe Bild 3.4.2) anschaulich zeigen, dass das Dipolmodell nicht genügt, um das reale Erdmagnetfeld hinreichend genau zu erklären. |
|
Der physikalische
Ansatz für ein sol-ches Dipolfeld besteht in einer
Be-trachtung des Magnetfeldes, einer so genannten Leiterschleife. Die mathematische Ableitung führt aber zu einer Differentialgleichung, in der ein elliptisches Integral auftaucht, für das keine geschlossene mathematische Lösung – in Form einer Gleichung – existiert. |
|
| Abbildung 4.0.2 – Leiterschleife |
| Der mathematisch allgemein
übliche Ansatz besteht darin, den auftretenden Term, im
Integral, in eine unendliche Reihe umzuwandeln: Vereinfacht lässt sich das so schreiben: |
![]()
| Dann geht man hin und schneidet diese Reihe nach dem ersten Glied einfach ab. Integriert man nun das Übriggebliebene, so entsteht die allgemeine Gleichung für das Dipolfeld, die praktisch nur von der geographischen Breite φ abhängig ist. |
| 4.0.1 - Gleichung: | 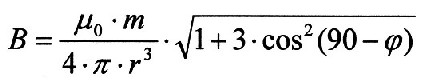 |
µ T |
| In der Gleichung steht B für die
magnetische Flussdichte, f für die geographische
Breite, m für das magnetische Moment, r
für den Erdradius und µ für die magnetische
Permeabilität. m, r, µ sind Konstanten die wie folgt definiert werden: Das
magnetische Moment ist in diesem Fall das magnetische
Moment der Erde mit m = 6,6845·1022
Am2 Für den Erdradius nimmt man den Wert aus einem geodätischen System, in diesem Fall das WGS84, dass diesen angibt mit: r = 6378155 m Die magnetische Permeabilität µ = 10-7 Vs/Am (Zur Ableitung des Dipolfeldes siehe z.B. auch "Berkeley Physik Kurs 2" von Edward Purcell, Seite 266-269) |
| Die hier dargestellte
mathematische Vorgehensweise zur Erreichung der
Dipolgleichung kann, aufgrund der abgeschnittenen
Restglieder, lediglich als eine erste Näherung betrachtet
werden. Fängt man an, die restlichen Glieder der unendlichen Reihe (aus der Leiterschleifenbetrachtung) zu integrieren, so erhält man das Quadrupolfeld, das Oktupolfeld usw. Insgesamt nennt sich das Multipolentwicklung. |
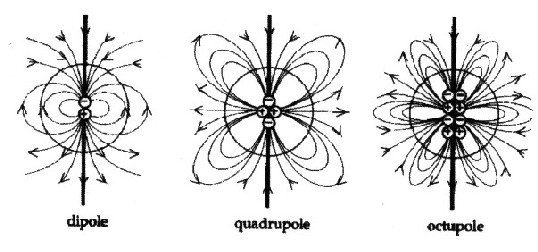
| Abbildung 4.0.3 – Multipolentwicklung |
| Siehe dazu „Gitterstrukturen des Erdmagnetfeldes“, Kapitel 1, Das Dipolfeld der Erde, Seite 17–23. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |