| Copyright © Klaus Piontzik | ||
| Englische Version |
| Für den Winkelanteil wird allgemein folgende Lösungsfunktion angegeben: |
| Gleichung 2.11.1.1 | 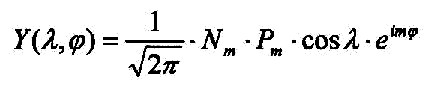 |
Es gilt: ei·mφ = cos(m·φ) + i·sin(m·φ) Die Nm und Pm sind die sogenannten Legendre-Polynome, die sich in dieser Betrachtung aber wie Konstanten handhaben lassen. Also insgesamt: |
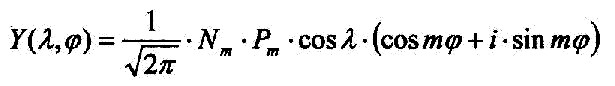
Multipliziert man die Klammer aus so ergibt sich:
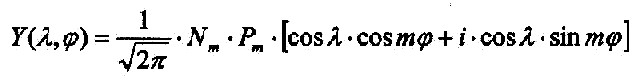
| Und
hier erkennt man wieder die multiplikativ verbundenen
Sinus- und Kosinusfunktionen, also tesserale
Kugelflächenfunktionen bzw. Gitter.
Hier nur mit einem realen und einem imaginären Anteil versehen, also eine komplexe Funktion als allgemeine Lösung des Winkelanteils der Laplace-Gleichung. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |