| Copyright © Klaus Piontzik | ||
| Englische Version |
| Mit der
Konstruktion des räumlichen Schwingungsgefüges steht
ein mathematisch/physikalisches Modell zur Verfügung,
dass es ermöglicht Strukturen der Erde auf einer Schwingungsbasis
zu erklären. Die Frage ist: Wie lautet
ein allgemein möglicher Ansatz für ein
Schwingungsgefüge? Pierre-Simon
(Marquis de) Laplace (28.03.1749 bis 05.03.1827)
war ein französischer Mathematiker, Physiker und
Astronom. Er arbeitete unter anderem auf den Gebieten der
Wahrscheinlichkeitstheorie und der
Differentialgleichungen. Der Laplace-Operator Nabla ist ein mathematischer Operator d.h. es handelt sich hier um eine allgemeine mathematische Vorschrift (Rechenweg). Der Laplace-Operator ist ein vektorieller Differentialoperator innerhalb der mehrdimensionalen Analysis. Der Laplace-Operator tritt beispielsweise in der Laplace-Gleichung auf. Zweimal stetig differenzierbare Lösungen dieser Gleichung heißen harmonische Funktionen. |
Laplace-Gleichung: |
| Gleichung 2.11.01 | |
| gelesen: Nabla f gleich null |
In kartesischen Koordinaten (x, y, z) ausgedrückt:
| Gleichung 2.11.02 | 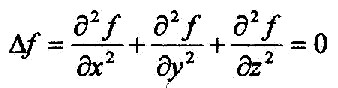 |
In nur einer Dimension gilt dann:
| Gleichung 2.11.03 | 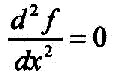 |
| Das ist
u.a. die Gleichung für einen harmonischen
Oszillator, also z.B. ein Pendel oder eine Feder
ohne Reibung. Die Laplace-Gleichung stellt somit eine mathematische Formel zur Beschreibung von Schwingungsphänomenen im Raum dar. Der allgemein übliche Ansatz für eine Lösung mit einer zentralen Konfiguration besteht darin die kartesischen Koordinaten (x, y, z) in Kugelkoordinaten (λ, φ, r) zu transformieren. Dann wird die gesamte Funktion in zwei Teilfunktionen zerlegt. Wobei eine Funktion den Winkelanteil und die andere Funktion den Radialanteil enthält. Der allgemeine Ansatz für eine Lösungsfunktion der Laplace-Gleichung in Kugelkoordinaten sieht dann so aus |
| Gleichung 2.11.04 | 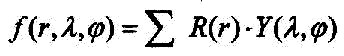 |
Die beiden Teilfunktionen R und Y lassen sich jeweils einzeln lösen.

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |