| Copyright © Klaus Piontzik | ||
| Englische Version |
 |
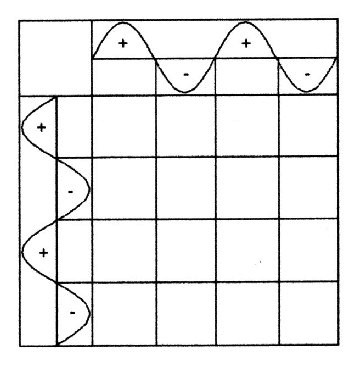 |
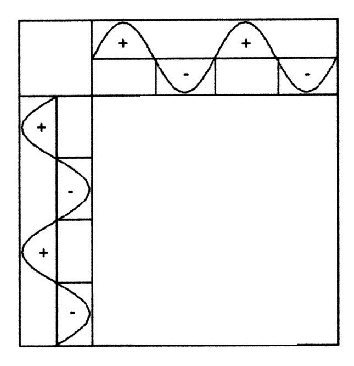
| Abbildung 2.2.1 – Nullgitter | |
| Die Nullpunkte der beiden Wellen werden auf die Betrachtungsebene übertragen, wie in Bild 2.2.1 rechts dargestellt. Dies entspricht einer tesseralen Kugelflächenfunktion mit: G0 = sin alpha · sin beta | |
| Zwei senkrechte Wellen lassen sich dann nach folgenden qualitativen Regeln addieren: |
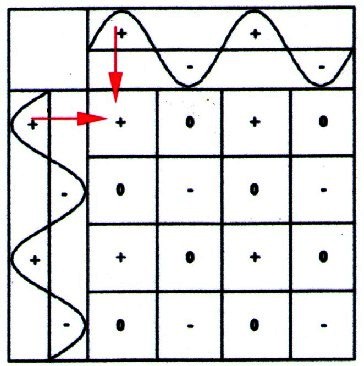 |
2.2.2 - Polbildung:1) + und + ergibt +2) – und – ergibt – 3) + und – ergibt 0 |
| Abbildung 2.2.2 – Multiplikation |
| Wie zu sehen ist, ergeben sich Felder mit verschiedenen Vorzeichen bzw. verschiedenen Zuständen. Es existieren insgesamt drei Schwingungszustände: positiv(+), negativ(-), neutral(0) |
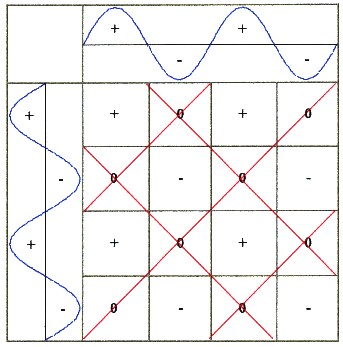 |
2.2.3 - Gitterbildung:Auffallend ist, dass alle Nullfelder diagonal zueinander liegen.Verbindet man nun die Nullfelder miteinander so ergibt sich das nebenstehende Bild. |
| Abbildung 2.2.3 – erzeugtes Gitter |
| 2.2.4 - Definition: | Das (rote)
gitterartige Gefüge heißt Grundfeld bzw. Gitter bzw. erzeugtes Feld. Die (blauen) erzeugenden Wellen heißen Grundschwingungen. Für das Grundfeld gilt: G = sin α + sin β |
| Während der mathematische
Begriff der Kugelflächenfunktion nicht nach der Ursache
des Schwingungsfeldes fragt, so müssen bei der
physikalischen Betrachtung die zugrunde liegenden Wellen
mit einbezogen werden. Dies leistet der Begriff des Grundfeldes. Das Grundfeld ist durch die Grundschwingungen definiert. Die Bezeichnungen Nullgitter und Grundfeld sind als physikalische ─quivalente zum mathematischen Begriff der tesseralen Kugelflächenfunktion zu sehen. |
| Die Multiplikation der Wellen
erfolgte wie gesehen zuerst in einer diskreten Art
und Weise. Bei einer kontinuierlichen also punktweisen Multiplikation zweier senkrecht aufeinander stehender Wellen ergeben sich Gittermuster, mit abwechselnden Polaritäten der Gitterfelder, wie in Abbildung 2.2.4 dargestellt. Hier zeigt sich, dass die Feldmaxima (Minima) in der Mitte der Quadrate punktförmig auftreten, während die Linien aus Nullwerten bestehen. Die Feldmaxima sind als Hügel zu erkennen, während die Täler durch die Feldminima gebildet werden. |
 |
 |
| Abbildung 2.2.4 – erzeugtes Gitter |
| Im linken Bild sind unten links und rechts die erzeugenden Schwingungen zu erkennen. Gut zu sehen ist auch, dass jeweils zwei erzeugte Gitterfelder wiederum eine (erzeugte) Schwingung ergeben. |
| 2.2.5 - Definition: | Gitter = zweidimensionales Schwingungsgefüge |
| Es ist möglich hier noch ein
zweites Gitter einzuzeichnen. Und zwar das Maximalgitter. Es verbindet die Feldmaxima und Minima, also die Hügelspitzen und die Talsohlen der Abbildung 2.2.4 und stellt den extremalen Verlauf des Feldes dar. Dies erlaubt zwei Sichtweisen des Gitters: |
| 2.2.6 - Definition: 1) das erzeugte Gitter wird in der Ebene der Grundschwingungen beschrieben: G = sin α + sin β 2) Das erzeugte Gitter wird in der Gitterebene selber beschrieben: G = sin φ · sin λ Beide Koordinatensysteme unterscheiden sich dadurch, dass sie um 45 Grad gegeneinander gedreht sind. Zur Illustration: Ein physikalisches Analogon zum Grundfeld bilden die |
| Chladni-Klang-Figuren |
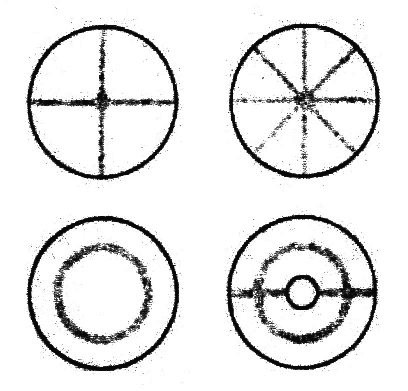 |
| Abbildung 2.2.5 – Chladni-Klangfiguren |
| Zur Erzeugung der Figuren wird
eine Metallplatte mit Sand bestreut und anschließend in
Schwingung versetzt. Bei bestimmten Frequenzen, den Eigenfrequenzen der Platte, tritt Resonanz auf und die gesamte Platte beginnt zu schwingen. Dabei bleibt der Sand genau an den Stellen liegen, an denen die Amplitude der Schwingung Null ist. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |