| Copyright © Klaus Piontzik | ||
| Englische Version |
| Nach Kapitel 2.1 besitzt eine
Kugel den Freiheitsgrad f = 3. Durch die
Verwendung von Kugelflächenfunktionen wären 2 Freiheiten
abgedeckt. Die dritte Freiheit, also die radiale Richtung, fehlt noch. Dazu wird das Verständnis einer physikalischen Darstellung benötigt, mit dem sich die Ausdehnung physikalischer Wellen beschreiben lässt: das huygensche Prinzip. Das huygensche Prinzip geht von einer Quelle S aus, die gleichförmig Wellenfronten nach allen Seiten hin erzeugt. Um die resultierende Wellenfront im Punkt P zu erhalten ist es aber nicht notwendig die gesamte Ausbreitung von S aus zu betrachten. Das huygensche Prinzip sagt, dass jeder Punkt (O) einer Wellenfront als Ausgangspunkt einer neuen Welle betrachtet werden kann, der sogenannten Elementarwelle. Die Lage der resultierenden Wellenfront in P ergibt sich durch Überlagerung (Superposition) sämtlicher Elementarwellen. |
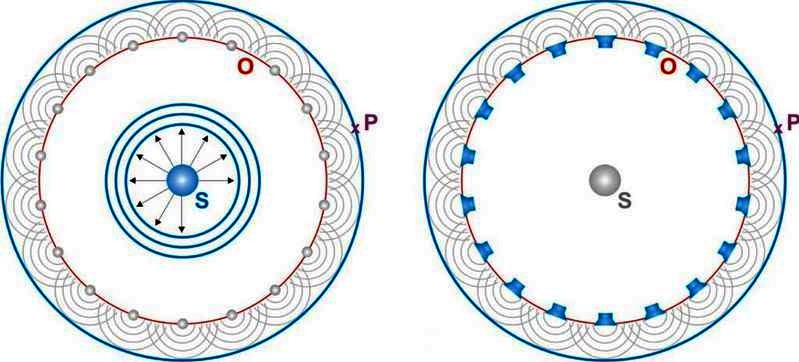
| Abbildung 2.3.1 – Huygensches Prinzip |
| Die Wellenursprünge (O)
liefern durch Superposition der Elementarwellen
die resultierende Wellenfront (P). In zwei Dimensionen sind Elementarwellen kreisförmig. In drei Dimensionen sind Elementarwellen kugelförmig. |
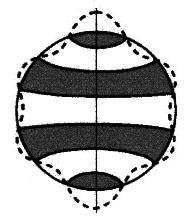 |
Anwendung des
huygenschen Prinzips für eine stehende Welle um eine
Kugel: Extremwerte der Welle = Quellen = Wellenursprünge 1 Schwingung = 2 Quellen |
| Abbildung 2.3.2 – Wellenursprünge |
| Das folgende Bild zeigt den Schwingungszustand für eine Schwingung nach dem huygenschen Prinzip mit einem Maximum (Wellenberg) als Quelle. |
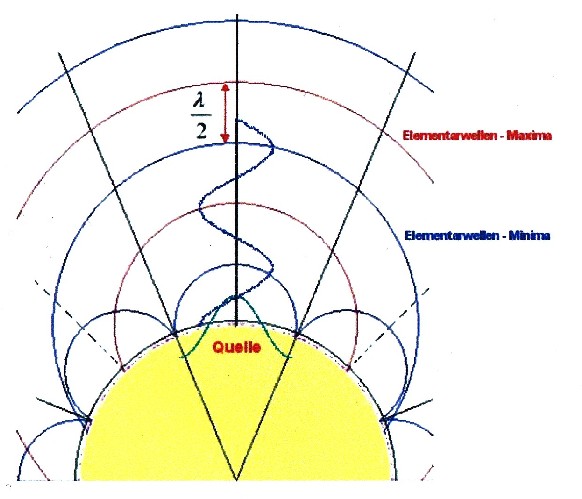 |
| Abbildung 2.3.3 – Elementarwellen |
| Da eine Welle aus Maxima und Minima besteht, bilden sich die Elementarwellen als Minimalfronten (blau) und Maximalfronten (rot) aus. Zwischen den Extremalfronten existieren natürlich auch noch Nullfronten. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |