| Copyright © Klaus Piontzik | ||
| Englische Version |
| Die bisherigen Betrachtungen erlauben nun eine erste Berechnung für eine Welle, die sich um eine Kugel z.B. die Erde herum aufbaut. Es muss noch berücksichtigt werden, dass die Wellenausbreitung linear stattfindet, und nicht entlang der gekrümmten Kugeloberfläche. |
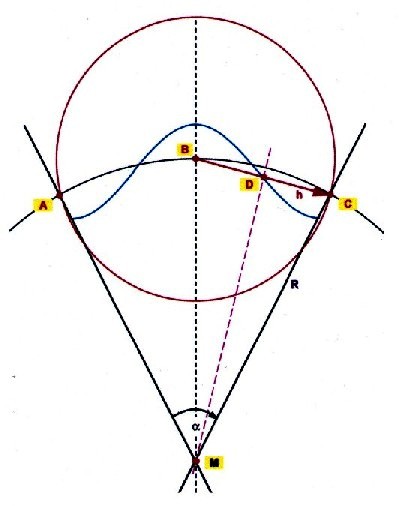 |
Nach dem Huygenschen Prinzip dienen die Punkte A, B, C
also die Extremalpunkte, als Quellpunkte der stehenden Welle (blau) Elektromagnetische Wellen breiten sich kugelförmig von einem Punkt aus. Wenn Punkt B der Ausgangspunkt ist, so entspricht die Strecke BDC = h dem Weg der Welle. |
| Abbildung 2.4.1 – Wellenausbreitung |
| Da ein stationärer Zustand herrscht, genügt es den Weg der Welle von einer Quelle zur nächsten Quelle zu betrachten. |
| Damit ist | 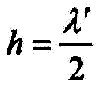 |
| Das Dreieck MCD im Bild ist rechtwinklig im Punkt D und es gilt: |
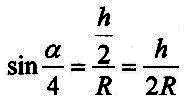 |
|
| Umstellen nach h ergibt: |
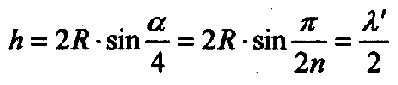 |
| Da jetzt alle Größen bekannt sind kann die Wellenlängen bestimmt werden: |
| 2.4.1 - Gleichung: | 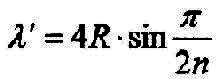 |
| In der Gleichung steht R
für den Radius der Erde, n für die
Anzahl der Schwingungen. Daraus ergibt sich die Frequenzgleichung für Grundschwingungen: |
| 2.4.2 - Gleichung: | 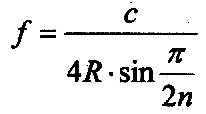 |
n = 1,2,3,4,... |
| Die Grundfrequenz ergibt sich für n = 1: |
2.4.3 -
Gleichung: 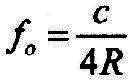 |
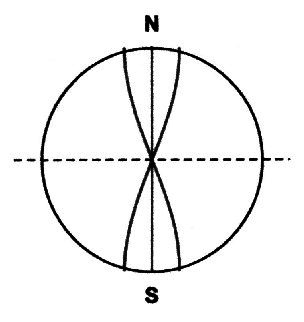 |
| Abbildung 2.4.2 – Grundschwingung |
| Dies entspricht auch der Schwingung eines Stabes mit freien Enden, dessen Länge gleich dem Durchmesser der Kugel ist. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |