| Copyright © Klaus Piontzik | ||
| Englische Version |
| Der Ansatz ist auch hier eine
Schwingungsbasis für das Erdmagnetfeld zu finden. Und es existiert bereits eine mathematische Methode, nämlich die Fourier-Analyse, mit der eine gegebene periodische Funktion in eine Summe von Sinus- und Kosinusfunktionen zerlegt werden kann. |

| Abbildung 4.5.1 – Totalintensität |
| Dazu wird die Graphik 4.5.1 für
die Totalintensität in eine Tabelle der
Totalintensitäten umgewandelt. So ist die Möglichkeit
einer Auswertung gegeben. Außerdem wird dadurch eine 3D-Darstellung des Erdmagnetfeldes an der Erdoberfläche möglich. Die Auswertung erfolgt hier über eine zweidimensionale Fourieranalyse. Da eine Fourieranalyse eine Zerlegung einer gegebenen Funktion in eine Summe von Sinus- und Kosinusfunktionen liefert, erhält man bei einer zwei-dimensionalen Fourieranalyse eine Summe von Kugelflächenfunktionen. Und beim Erdmagnetfeld gelingt es tatsächlich eine Zerlegung in Kugelflächenfunktionen vorzunehmen. |
| Das Gesamtfeld wird in einzelne -
in diesem Fall in horizontale Schnitte zerlegt. Mit jedem
Schnitt lässt sich eine eindimensionale Fourier-Analyse
ausführen. Jeder Schnitt verläuft quasi entlang eines Breitenkreises. Von +90 Nord bis –90 Süd werden die Schnitte im Abstand von 7,5 Grad angelegt. Dies ergibt dann 25 Schnitte. (7,5 Grad = 800 Km) Jeden Schnitt unterzieht man einer eindimensionalen (numerischen) Fourier-Analyse, mit der Variablen l und der Schrittweite 7,5 Grad, d.h. mit 48 Punkten pro Schnitt. Es ergeben sich so insgesamt 1106 Punkte für die Analyse des Erdfeldes. Als Grundlage bzw. Werkzeug der gesamten Analyse dient ein numerisches (eindimensionales) harmonisches Verfahren, wie es im Buch „Mathematik für Ingenieure“ von Brauch/Dreyer/Haacke beschrieben wird und auch als Algorithmus von Goertzel (und Reinsch) bekannt ist. Dann lassen sich die 25 Schnitte, durch die Fourieranalyse bedingt, allgemein so darstellen: |
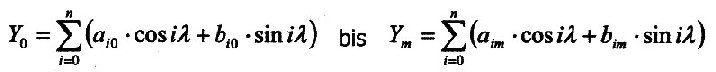
| Es entsteht ein Gleichungssystem
von m+1 Gleichungen mit jeweils n+1
Gliedern. Über die erzeugte Koeffizientenmatrix mit den Am und Bm kann eine weitere Fourier-Analyse, mit der Variablen phi durchgeführt werden. Für jeden Punkt auf der Erde mit den Koordinaten λ, φ gilt dann: |
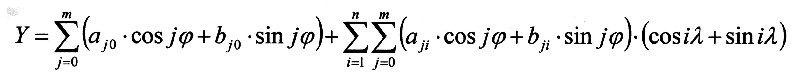
| Das gesamte Verfahren der Fourier-Analyse sieht dann so aus: |
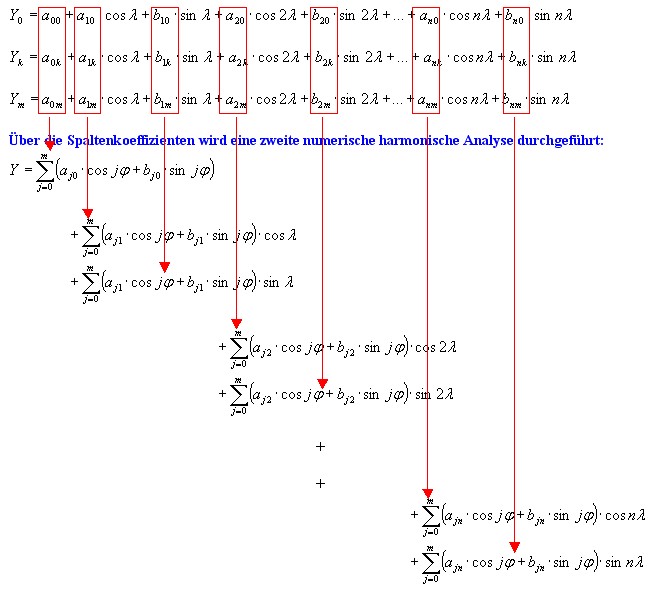
| Der erste Term für Y (also der zonale, sektorielle Teil) lässt sich noch so ergänzen: |
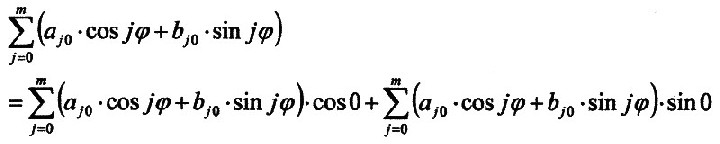
| Durch die quantitative Analyse
einerseits und dem mathematischen Verfahren andererseits
bedingt, lässt sich folgende Gesamtgleichung für die magnetische
Flussdichte an der Erdoberfläche erstellen: 4.5.1.1 - Gleichung: |
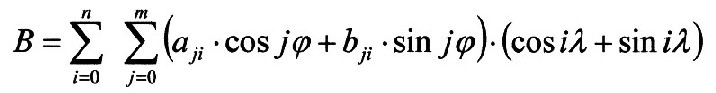
| Löst man die Klammern hinter der Doppelsumme auf, so treten nur tesserale Kugelflächenfunktionen also Gitter auf. |
| 4.5.1.2 - Satz: | Das Magnetfeld der Erde (an der Erdoberfläche) lässt sich vollständig durch eine Summe von Gittern beschreiben. |
| Gleichzeitig stellt diese Funktion eine Lösung des Winkelanteils der Laplace-Gleichung dar. In der Konsequenz gilt dann: |
| 4.5.1.3 - Satz: | Magnetfeld der
Erde (an der Erdoberfläche) = zweidimensionales Schwingungsgefüge |
| Hier entsteht die Frage ob ein
Zusammenhang zwischen dem zwei-dimensio-nalen
magnetischen Schwingungsmodell und dem
Erd-Schwingungsgefüge existiert? Aufgrund des allgemeinen Ansatzes der Fourier-Analyse und Gleichung 4.5.1.1 lässt sich noch folgende allgemeine Aussage machen: |
| 4.5.1.4 - Satz: | Jedes Schwingungsgefüge um eine Kugel lässt sich vollständig durch eine Summe von tesseralen Kugelflächenfunktionen beschreiben. |
| Mit Kapitel 2.11.1 lässt sich sogar formulieren: |
| 4.5.1.5 - Satz: | Jedes Schwingungsphänomen um eine Kugel lässt sich als Lösung des Winkelanteils der Laplace-Gleichung darstellen. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |