| Copyright © Klaus Piontzik | ||
| Englische Version |
| Die einzelnen Teile, aus der
Fourier-Analyse (Kugelflächenfunktionen), erlauben eine
graphische Darstellung der magnetischen Gesamtsituation. In die Karte der Totalintensität werden alle Extremwerte, magnetischen Strukturen und Quellpunkte eingetragen, die sich durch die Fourier-Analyse ergeben, wie in der Abbildung 4.6.1 zu sehen ist. |
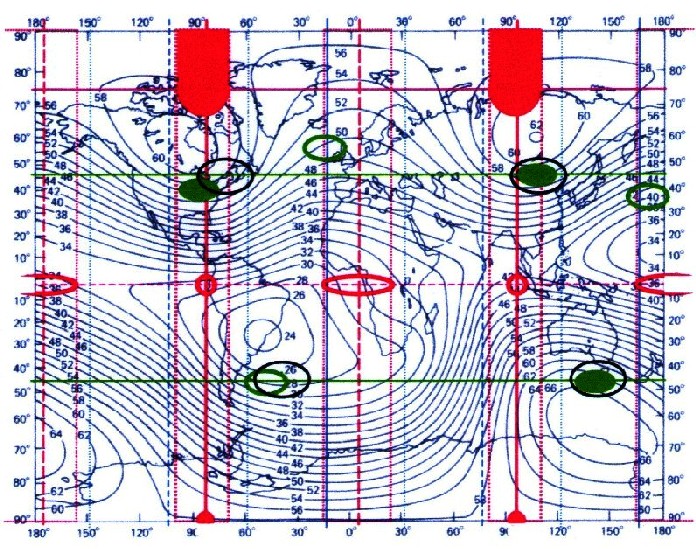
| Abbildung 4.6.1 - Erdmagnetfeld |
| Es gilt für die Farbzuweisung in
Abbildung 4.6.1: Blau – dreiachsiges Ellipsoid Rot – Zonal, Sektoriell (Gitter ZS) Grün – Tesseral Schwarz – hyugensche Quellpunkte Aus der Abbildung 4.6.1 ergeben sich Zusammenhänge, die auf den nächsten Seiten detailliert dargestellt werden. Dabei handelt es sich um die Beziehungen des Erdmagnetfeldes zur Erdgestalt, die Auswirkungen des Gitter ZS auf die magnetischen Verhältnisse in der Arktis, sowie die Lage des tesseralen Feldes und die Position der huygenschen Quellpunkte. |
| Mit Hilfe der Satellitengeodäsie sind 1966 durch C.A. Lundquist und G. Veis folgende Parameter ermittelt worden, um die Erde als echtes dreiachsiges Ellipsoid darzustellen: |
| a1
- a2
= 69 Meter λ0 = -14,75 Grad West |
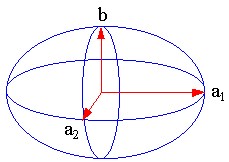
| Abbildung 4.6.1.1 - Dreiachsiges Ellipsoid |
| Das blaue
Ellipsoidgitter, in Abbildung 4.6.1, orientiert sich an
den Werten von Lundquist und Veis und ist zum roten magnetischen System um 1,25 Grad
verschoben. Global gesehen ist also eine gute ▄bereinstimmung festzustellen. Eine Analyse der geographischen Positionen aller auftretenden magnetischen Extrema, ergibt einen funktionalen Zusammenhang für deren geographische Länge, die Längenpositionsgleichung. Die Ableitung der folgenden Gleichung ist im Buch „Gitterstrukturen des Erdmagnetfeldes“, Kapitel 4.4, Der Nullpunkt, Seite 39–41 und Kapitel 9.5, Das Gitter ZS, Seite 70–71, zu finden. Siehe dazu auch „Gitterstrukturen des Erdmagnetfeldes“, Kapitel 17, Die Gestalt der Erde, Seite 146–158. |
| 4.6.1.1 - Gleichung: | m ist Element der ganzen Zahlen (...-2,-1,0,1,2,...) |
| 4.6.1.2 - Satz: | Das Erdmagnetfeld steht in Relation zur Erdgestalt. |
| Das rote magnetische
System in der Abbildung 4.6.1 stellt das Gitter
ZS, also den zonal-sektoriellen Anteil
dar. In der Gleichung 4.5.2.1 taucht, im zonalen Anteil, der Term 11,3642 cos 2φ auf. Dies entspricht dem Dipol-Anteil des Erdfeldes. Der Dipolanteil macht etwa 84 % des Gesamtfeldes aus. Da hier noch die sektoriellen Anteile hinzu kommen, entsteht ein magnetischer Rücken am Nordpol, während am Südpol nur eine punktförmige Maximalzone vorhanden ist. |
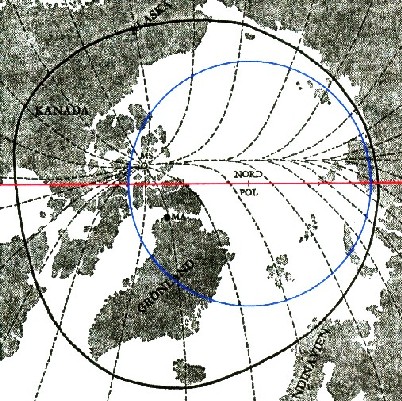 |
Die Abbildung zeigt die Nordlichtzone (schwarzer Kreis) und die geo-magnetischen Verhält-nisse in der Arktis.Eingetragen sind die zonale (blauer Kreis) und die sektorielle (rote Linie) Maximalzone. Durch Addition des zonalen mit dem sekto-riellen Anteil lässt sich der magnetische Rücken in der Arktis erklären. | |
| Abbildung 4.6.2.1 - Magnetische Verhältnisse in der Arktis |
| Der magnetische Rücken stellt die
Maximalzone des Grundfeld ZS dar. Die zonale Maximalzone
reicht vom Pol bis zu etwa 67░
nördlicher Breite. Dies stimmt gut mit der Polarlichtzone
überein. Das magnetische Feld, am nördlichen Polarkreis, wird hauptsächlich durch das Grundfeld ZS geprägt Die Maximumzone = magnetischer Hauptmeridian (dick rot), in Abbildung 4.6.1, ist gut zu erkennen, und zwar bei Lambda = – 83,5░ West und Lambda = 96,5░ Ost. Die Minimumzonen (rot gestrichelt) liegen bei Lambda = 5,25░ Ost und bei Lambda = – 174,25░ West. Die globalen Verhältnisse des Gitter ZS sind noch einmal in Abbildung 4.6.2.2 dargestellt. Die blauen senkrechten Linien stellen die Hauptachsen für einen dreiachsigen Ellipsoid dar. |
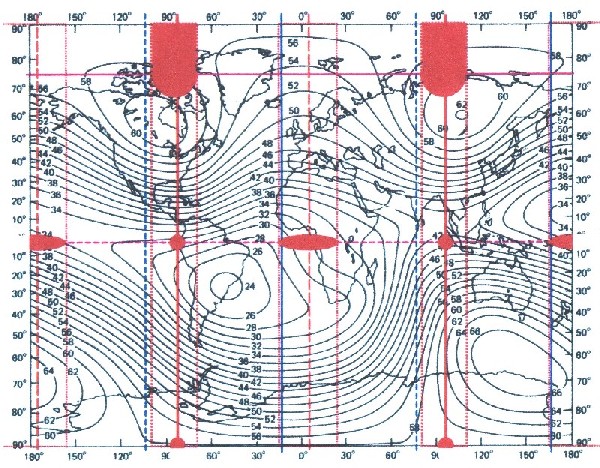
Abbildung 4.6.2.2 - Grundfeld ZS
| In der ─quatorebene befinden sich
zwei Minimalzonen (rote Ellipsen) und
zwei Sattelpunkte (rote Kreise), mit
jeweils 90 Grad Abstand. Siehe dazu auch „Gitterstrukturen des Erdmagnetfeldes“, Kapitel 9.2–9.7, Seite 64–72. |
| 4.6.2.1 - Satz: | Alle Extremwertzonen des Gitter ZS liegen auf den Ecken eines Oktaeders. |
| Abbildung 4.6.2.3 – Oktaeder |
| Siehe dazu auch „Gitterstrukturen des Erdmagnetfeldes“, Kapitel 9.2–9.7, Seite 64–72. |
| Das grüne System, in Bild 4.6.1, stellt den tesseralen
Anteil dar. Alle Extremwerte liegen etwa bei ▒45░
Breite. Die grünen Punkte stellen die Maximal- bzw. Minimalpunkte des reinen (tesseralen) Gitteranteils des Erdmagnetfeldes dar. Die globalen Verhältnisse des tesseralen Feldes sind noch einmal in Abbildung 4.6.3.1 dargestellt. Vollgrün = Maximum Grün Umrandet = Minimum |
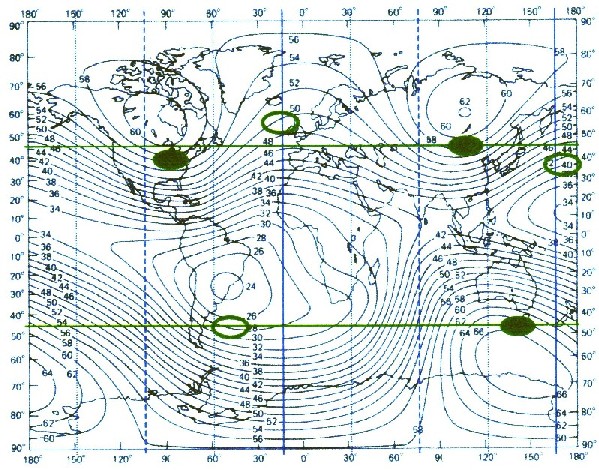
Abbildung 4.6.3.1 - Tesserale Extrema
| Die blauen senkrechten Linien stellen die Hauptachsen für einen
dreiachsigen Ellipsoid dar. Auf der Nordhalbkugel liegen alle Extremwerte annähernd auf einem Quadrat. Die Extremalzonen, auf der Südhalbkugel, sind um etwa 35-40░ gegenüber den nördlichen Extremalzonen verschoben. Durch die 45░ Breite wird koordinatenmäßig, in der Erde, ein verdrehter Spat (Kubus) aufgespannt. |

| Abbildung 4.6.3.2 – Kubus |
| 4.6.3.1 - Satz: | Die Extremwertzonen des tesseralen Feldes liegen auf den Ecken eines verdrehten Kubus. (Spat) |
| Siehe dazu auch
„Gitterstrukturen des Erdmagnetfeldes“, Kapitel
9.8, Der tesserale Anteil, Seite 73–75. Der tesserale Anteil ist nahezu identisch mit dem non-Dipol-Feld, welches etwa 16% des gesamten Erdmagnetfeldes ausmacht. Wie beim Gitter ZS gilt auch für den tesseralen Anteil die Längenpositionsgleichung 4.6.1.1 für die Extremalwerte. |
| Die Schwarz
umrandeten Ellipsen, in Bild 4.6.1, stellen die huygenschen
Quellpunkte des Gesamtfeldes dar. Das Grundfeld- bzw. Gittermodell und das Huygensche Prinzip vorausgesetzt, stellen diese vier Pole die theoretischen Quellpunkte dar, von denen aus sich das gesamte äußere magnetische Feld an der Erdoberfläche aufspannen lässt. Die Quellpunkte liegen auf den Ecken eines Tetraeders. Dagegen sind die Quellen auf der Südhalbkugel um 45░ verschoben. |
| Abbildung 4.6.4.1 – Tetraeder |
| 4.6.4.1 - Satz: | Die huygenschen Quellpunkte liegen auf den Ecken eines verdrehten Tetraeders. |
| Es herrscht
▄bereinstimmung der Quellbereiche mit den vier
Hauptextrema des tesseralen Feldes. Siehe dazu auch „Gitterstrukturen des Erdmagnetfeldes“, Kapitel 11.7, Die Bestimmung der Quellpunkte, Seite 91. Die globalen Verhältnisse der huygenschen Quellpunkte sind noch einmal in Abbildung 4.6.4.2 dargestellt. Die durchgezogenen roten, senkrechten Linien stellen den magnetischen Hauptmeridian dar. |

Abbildung 4.6.4.2 – Huygensche Quellpunkter
| Laut der numerischen
Fourier-Analyse beträgt der statische Anteil des
Erdfeldes in Gleichung 2.5.2.1 47,2183 uT.
Der minimalste Wert des Feldes liegt bei 24 uT, der maximalste Wert beträgt 62 uT. Daraus erklärt sich, dass sich etwa 75 % des Feldes wie ein permanenter Magnet verhalten, d.h. nur 25 % des Feldes bilden das magnetische Schwingungsgefüge. Alle Extremwertzonen des Gitter ZS liegen auf den Ecken eines Oktaeders. Die Extremwertzonen, des tesseralen Feldes, liegen auf den Ecken eines verdrehten Kubus, bzw. eines Spat. Die huygenschen Quellpunkte des Feldes liegen auf den Ecken eines verdrehten Tetraeders. Die magnetische Extrema sind in Form der einfacheren platonischen Körper (Tetraeder, Kubus, Oktaeder) angeordnet. Bemerkung: Ein Parallelepiped (Synonyme: Spat, Parallelflach, Parallelotop) ist ein geometrischer Körper, der von sechs Parallelogrammen begrenzt wird. Die Bezeichnung Spat stammt vom Kalkspat ab, dessen Kristalle die Form eines Paralelepipeds besitzen. Das Erdmagnetfeld steht in Relation zur Erdgestalt. Das Ellipsoidgitter ist zum magnetischen System nur um 1,25 Grad verschoben. Eine Analyse aller auftretenden magnetischen Extrema ergibt einen funktionalen Zusammenhang, für deren geographische Länge: |
| 3,75 Grad <=> 96er Teilung |
| Durch die 96er-Teilung ist eine ausreichende Differenzierung vorhanden, um alle auftretenden Winkel für Polyeder, bzw. für die platonischen Körper, zu enthalten. |
| 4.6.5.1 - Satz: | Alle Platonischen Körper sind als Schwingungsfiguren des Erdschwingungsgefüges möglich. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |