Synthese

	Planetare Systeme der Erde 1 Klassische Systeme

	Copyright © Klaus Piontzik


Englische Version

Wenn erdmagnetische Wellen existieren, lässt sich noch folgender Schluss ziehen: Nach Kapitel 3.9, Gleichung 3.9.2 gilt für alle Schichten der Erde:

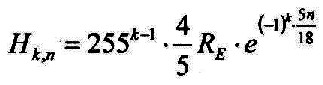
Es sei:
6.5.1 Definition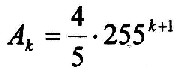

Es sei:
6.5.2 Definition

So lässt sich allgemein für die Radialstruktur schreiben:

Nach Kapitel 4.5.1, Gleichung 4.5.1.1 gilt für den Winkelanteil des Feldes:

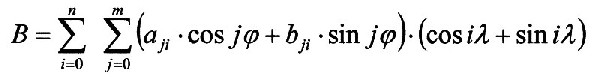
Nach Kapitel 2.11, Gleichung 2.11.04 besteht die Gesamtlösung der Laplace-Gleichung aus der Multiplikation der Einzellösungen, also dem Radialanteil und dem Winkelanteil.

6.5.1 - Gleichung:

S(r, λ, φ) = A_k × R_E × e^qn × B

Dann lässt sich allgemein, für ein Erdschwingungsgefüge, folgende Gleichung formulieren, die auch gleichzeitig eine Lösung der Laplace-Gleichung darstellt:

6.5.2 - Gleichung:

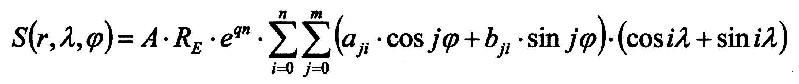
Der Radialanteil besitzt die Maßeinheit Meter. Der Winkelanteil besitzt die Maßeinheit Ampere pro Meter. Damit in der Lösungsfunktion die Maßeinheiten wieder stimmen, muss die Lösungsfunktion, bzw. der Radialanteil noch normiert werden. Die normierte Gleichung sieht dann so aus.

6.5.3 - Gleichung:

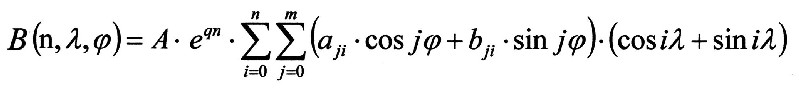
Dies ist als alternative Formulierung zur Gleichung 4.1.1 bzw. 4.1.2 von Gauß und Weber zu verstehen, da die Gleichung 6.5.3 deutlicher den Schichten- und Schwingungs-Charakter des Feldes zum Ausdruck kommt.
Wohin gegen die Gleichungen von Gauß und Weber mehr den Vektorcharakter des Feldes beschreiben.

Das Erdmagnetfeld spielt im Erdschwingungsgefüge eine zentrale Rolle. Zum einen hat es bei der Auskristallisierung der geologischen Schalen, zu Polyederstrukturen in der Erde, geführt.
Zum anderen ist es noch heute an der Aufrechterhaltung der elekt-risch leitfähigeren Schichten der Atmosphäre und damit des elektrischen Feldes der Erde beteiligt.
Diesen Zusammenhang bedingt, dass das Magnetfeld einen mitgestaltenden Faktor bei Wetter- und Klimabildung einbringt.

bei Amazon kaufen

284 Seiten, davon 44 in Farbe
220 Bilder
57 Tabellen

Herstellung und Verlag:
Books on Demand GmbH, Norderstedt

ISBN 978-3-7494-8112-5

Ladenpreis: 17,50 Euro

6.5 - Synthese