| Copyright © Klaus Piontzik | ||
| Englische Version |
| Der amerikanische Physiker James
Bjorken fand 1969, dass offenbar eine logarithmische
Skaleninvarianz in den Häufigkeits-Verteilungen der
Elementar-Teilchen in Abhängigkeit von ihrer Ruhemasse
existiert (Bjorken, Feinmann). Im Jahr 1987 erweiterte Hartmut Müller die Entdeckungen für alle bekannten Teilchen, Kerne und Atome sowie Asteroiden, Monde, Planeten und Sterne. Die Global-Scaling-Theorie soll Strukturierungs-Phänomene der Materie im Universum beschreiben. Global Scaling Definition: Die Grundlage der Theorie kann wie folgt zusammengafasst werden: Wenn beliebige quantitative Eigenschaften natürlicher Systeme, also Frequenzen, Größen, Massen, Lebensdauer u.s.w. von Elementen, Atomen, Molekülen, Zellorganellen, Zellen, Organen, Organismen, Populationen, Monden, Planeten, Sternen oder Galaxien auf einer logarithmischen Skala angeordnet werden, dann sind diese Werte nicht gleichmäßig verteilt, sondern häufen sich in bestimmten Zonen, während andere Zonen fast leer bleiben. Dabei wird ein sogenanntes Eichmaß benutzt um eine entsprechende Skalierung zu rewährleisten. Das Global-Scaling-Konstrukt war jahrelang Hintergrund für Betrügereien und die Vermarktung diverser Scharlatanerieprodukte und fragwürdiger Dienstleistungen wie etwa Lottovorhersagen. Der Erfinder Hartmut Müller wurde wegen Betruges zu einer mehrjährigen Haftstrafe verurteilt. Dabei wurde auch Global Scaling als ein pseudowissenschaftlich-esoterisches Konglomerat eingestuft. Bei Psiram und anderen Seiten im Internet wird Global Scaling als Pseudo-Wissenschaft dargestellt, jedoch bleiben alle diese Seiten schuldig einen Beweis dazu zu liefern. Hier ist nun der mathematische Beweis, das die Wahl des Eichmaßes im Global Scaling rein willkürlich ist und damit die Global-Scaling-Theorie zumindest überflüssig ist bzw. das Global-Scaling ein willkürlich spekulatives Konstrukt darstellt. |
| Es sind n
Werte gegeben, nämlich: w0,
w1, w2,
... wk, ... wn Es existieren Eichwerte: Meich im Global Scaling die auf den physikalischen Größen des Protons beruhen. Die Skalierung im Golbal Scaling wird durch folgende Gleichung definiert: |
| 7.7.1 - Gleichung: |
|
| Aufgrund der Logarithmen-Gesetze gilt: |
|
| Nach Gleichung 7.4.5 gilt: |
|
| So lässt sich schreiben: |
|
| Einsetzen des Terms für y: |
|
| Nach Gleichung 7.4.4 gilt auch: |
|
| Insgesamt ergibt sich: | |
| 7.7.2 - Gleichung: |
|
| Einsetzen aller Terme ergibt: | |
| 7.7.3 - Gleichung: |
|
Wenn das Eichmass gleich 1 (Meich = 1) gesetzt wird, so entsteht einfach die Gleichung 7.4.5: Sk = yk = axk+b Das bedeutet: 1) Es besteht ein funktionaler Zusammenhang zwischen der hier geschilderten Prozedur der e-Funktions-Findung und dem Global Scaling. 2) Die hier geschilderte Prozedur liefert eine Form der Skalierung, die fundamentaler Natur ist, während das Global Scaling eine eher abgeleitete Größe darstellt, weil dort ein bestimmtes Eichmaß benutzt wird. Das lässt sich daran erkennen, dass in der Gleichung 7.7.2 das Eichmass lediglich in der additativen Komponente der Geradengleichung vorkommt. Sind alle Werte gegeben, stellt dieser Term lediglich eine additative Konstante dar. Der eigentliche Skalierungsvorgang findet aber im ersten Term statt. Man kann das auch noch so darstellen: Die additative Konstante erhält einen neuen Namen: 7.7.4 - Definition: |
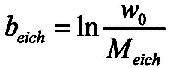
Dann lässt sich die Skalierungsfunktion auch so darstellen: 7.7.5 - Gleichung: |
![]()
| D.h. wir
haben hier eine Geradengleichung vor uns. Die Steigung
der Geraden wird durch den ersten Term ax
dargestellt. Die additative Konstante b verschiebt
diese Gerade lediglich in der Senkrechten, also entlang
der y-Achse. 3) Die hier geschilderte Prozedur ist ein Äquivalent zum Global Scaling. Damit wird das Global Scaling noch mal bestätigt, hinsichtlich der logarithmischen Struktur des Universums (siehe auch Kapitel 8). Allerdings zeigen die Gleichungen 7.7.2 und 7.7.4 das die Wahl des Eichmaßes beliebig ist. Statt der Protonengrößen im Global Scaling lässt sich auch jede andere Größe wie z.B. das Elektron benutzen. Mathematisch
viel natürlicher ist es, das Eichmass gleich 1
(Meich = 1) zu
setzen. Als
Beispiel dienen hier die Planetenbahnen. In der Tabelle
ist die Ursprungsnummerierung (alt) enthalten, sowie die
genäherte Nummerierung aus der Linearisierung und die
berechnete Nummerierung. |
| Planet | Nr | Abstand | Nr | xk | a·xk | Global Scaling |
| alt | [AE] | genähert | berechnet | a·xk+beich | ||
Merkur |
0 |
0,3871 |
0 |
0 |
0 |
60,88009872 |
Venus |
1 |
0,723 |
1,3 |
1,182 |
0,624726165 |
61,50482488 |
Erde |
2 |
1 |
1,9 |
1,796 |
0,949072221 |
61,82917094 |
Mars |
3 |
1,524 |
2,6 |
2,593 |
1,370410679 |
62,25050940 |
Asteroiden |
4 |
2,7 |
3,75 |
3,675 |
1,942323994 |
62,82242271 |
Jupiter |
5 |
5,203 |
5 |
4,916 |
2,598307604 |
63,47840632 |
Saturn |
6 |
9,582 |
6,1 |
6,071 |
3,208958560 |
64,08905728 |
Uranus |
7 |
19,201 |
7,5 |
7,386 |
3,904034582 |
64,78413330 |
Neptun |
8 |
30,047 |
8,25 |
8,233 |
4,351835044 |
65,23193376 |
Pluto |
9 |
39,482 |
8,75 |
8,750 |
4,624917093 |
65,50501581 |
| Im Global
Scaling wird die Eigenwellenlänge des Protons mit einem
Wert von 2,103089 10-16
m als Eichmaß angegeben. Damit ergibt sich beich
= 60,88. Für die Planetenbahnen gilt: a = 0,52856 (siehe Seite 176) Die
berechneten Nummerierungswerte xk
spiegeln die absoluten harmonikalen Verhältnisse eines
Systems wieder und sind von einem Eichmaß völlig unabhängig.
Auch hier in diesem Kapitel kann man in allen Gleichungen ln durch log ersetzen. So gilt dann die gesamte Betrachtung und Funktionsermittlung auch zur Basis 10. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |