| Copyright © Klaus Piontzik | ||
| Englische Version |
| Unser Sonnensystem besitzt mit den Planetenbahnen ebenfalls eine konzentrische Struktur. Es werden die Abstände in astronomische Einheiten (AE) für die ersten 8 Planeten aus der gängigen Literatur zusammen getragen. Hierbei werden die einzelnen Planeten nach Abstand geordnet und durchnummeriert. |
| Planet | Nr | Abstand | ln(Abstand) |
| (AE) | |||
Merkur |
0 |
0,3871 |
-0,94907222 |
Venus |
1 |
0,723 |
-0,32434606 |
Erde |
2 |
1 |
0 |
Mars |
3 |
1,524 |
0,42133846 |
Jupiter |
4 |
5,203 |
1,64923538 |
Saturn |
5 |
9,582 |
2,25988634 |
Uranus |
6 |
19,201 |
2,95496236 |
Neptun |
7 |
30,047 |
3,40276282 |
AE = astronomische Einheit = 149.597.870 Km = Abstand Erde - Sonne Aus der Tabelle ergibt sich die folgende Funktion y für die Logarithmen der Abstände: |
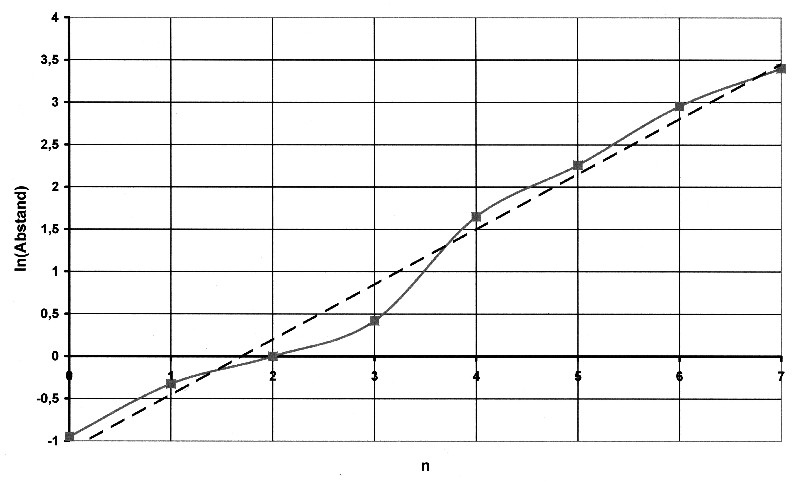
Abbildung 8.2.1 – Logarithmierte Planetenbahnen
| Die
gestrichelte Linie im Diagramm stellt eine Näherungsgerade
dar. Wie zu sehen existiert schon eine gute
Linearität der Werte. |
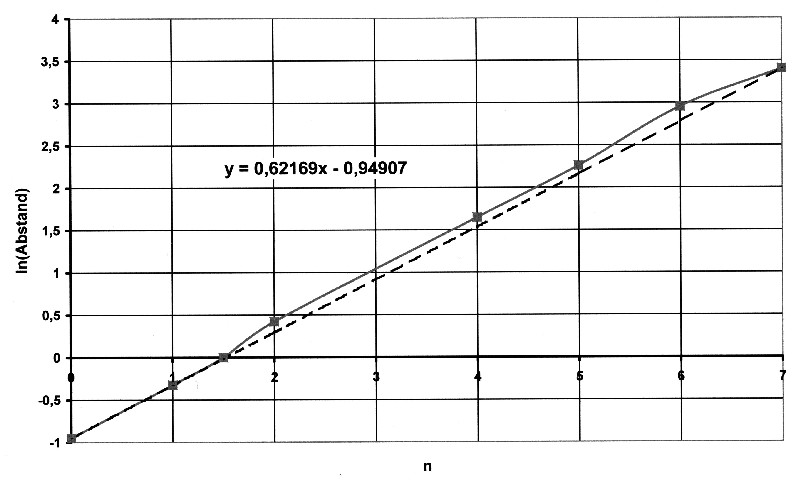
Abbildung 8.2.2 – Linearisierung
| Mit dem
gleichen Verfahren wie bei den Sonnenschalen beschrieben
werden die Parameter der Näherungsgeraden ermittelt. Die Gleichung für die Näherungsgerade lautet: y = 0,62169 · x – 0,94907 Für die Planetenbahnen gilt: Abstand = 0,3871 · e0,62169x [AE] Damit ergeben sich folgende Werte: |
| Planet | Nr | Abstand | Abstand |
| [AE] | [AE] | ||
| berechnet | |||
Merkur |
0 |
0,3871 |
0,3871 |
Venus |
1 |
0,723 |
0,7208087 |
Erde |
1,5 |
1 |
0,98359983 |
Mars |
2 |
1,524 |
1,34219887 |
Jupiter |
4 |
5,203 |
4,65383058 |
Saturn |
5 |
9,582 |
8,66577519 |
Uranus |
6 |
19,201 |
16,1363114 |
Neptun |
7 |
30,047 |
30,047 |
Die gesamte Situation für die Planetenbahnen sieht dann so aus:
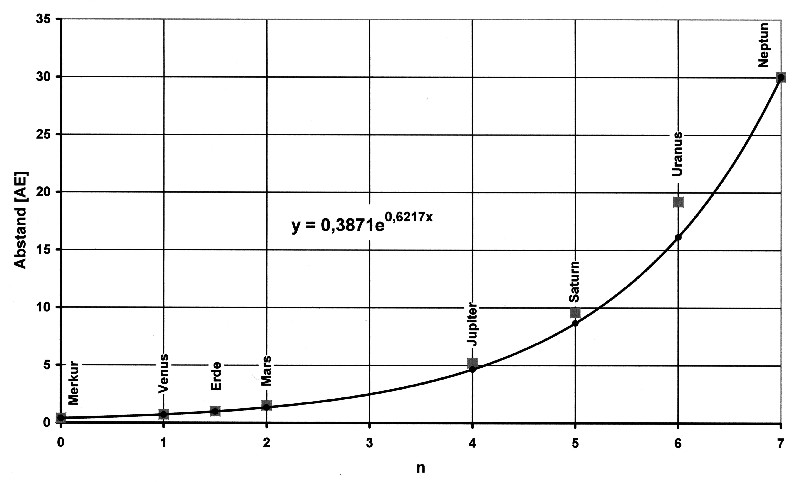
Abbildung 8.2.3 – Planetenbahnen als e-Funktion
| Bemerkenswert
ist die Lücke für n = 3. Der
Abstandswert dazu beträgt 2,5 AE. Der Asteroidengürtel erstreckt sich von 2,0 bis 3,4 AE. Der Mittelwert liegt bei 2,7 AE. Damit deckt sich das Modell sehr gut mit den realen Begebenheiten. Und es zeigt, dass der Asteroidengürtel mit zum Schwingungssystem der Planeten gehört. Und es zeigt auch das die Prozedur der Logarithmierung und Linearisierung kein willkürlicher Akt ist, sondern die harmonikalen Strukturen eines Systems offenbart. Daher wird hier ein neuer Ansatz generiert, diesmal mit dem Asteroidengürtel und Pluto dazu. |
| Planet | Nr | Abstand | ln(Abstand) |
| (AE) | |||
Merkur |
0 |
0,3871 |
-0,94907222 |
Venus |
1 |
0,723 |
-0,32434606 |
Erde |
2 |
1 |
0 |
Mars |
3 |
1,524 |
0,42133846 |
Asteroidengürtel |
4 |
2,7 |
0,99325177 |
Jupiter |
5 |
5,203 |
1,64923538 |
Saturn |
6 |
9,582 |
2,25988634 |
Uranus |
7 |
19,201 |
2,95496236 |
Neptun |
8 |
30,047 |
3,40276282 |
Pluto |
9 |
39,482 |
3,67584487 |
Aus der Tabelle ergibt sich die folgende Funktion für die Logarithmen der Abstände:
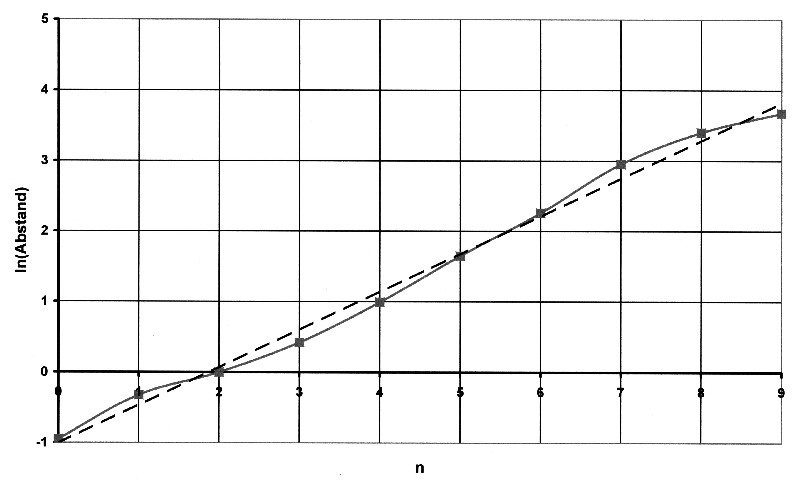
Abbildung 8.2.4 – Logarithmierte Planetenbahnen
| Die gestrichelte Linie im Diagramm stellt wieder eine Näherungsgerade dar. Wie zu sehen ist, existiert schon ein sehr gutes Linearitätsverhalten der Werte. Die Werte werden noch linearisiert und ergeben so folgendes Diagramm: |
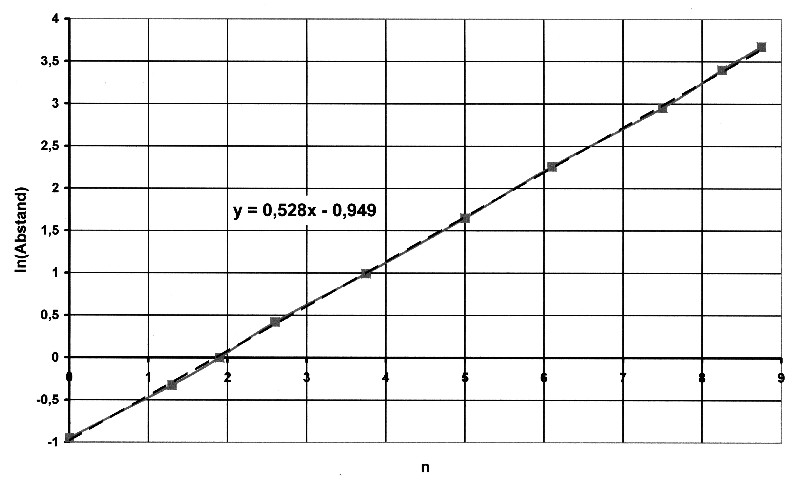
Abbildung 8.2.5 – Linearisierung
| ie
Gleichung für die Näherungsgerade lautet: y =
0,52856 · x – 0,94907 Für die Planetenbahnen gilt: Abstand = 0,3871 · e0,52856x[AE] Damit ergeben sich folgende Werte: |
| Planet | Nr | Abstand |
| neu | [AE] | |
Merkur |
0 |
0,3871 |
Venus |
1,3 |
0,723 |
Erde |
1,9 |
1 |
Mars |
2,6 |
1,524 |
Asteroidengürtel |
3,75 |
2,7 |
Jupiter |
5 |
5,203 |
Saturn |
6,1 |
9,582 |
Uranus |
7,5 |
19,201 |
Neptun |
8,25 |
30,047 |
Pluto |
8,75 |
39,482 |
Die neue Situation für die Planetenbahnen sieht dann so aus:
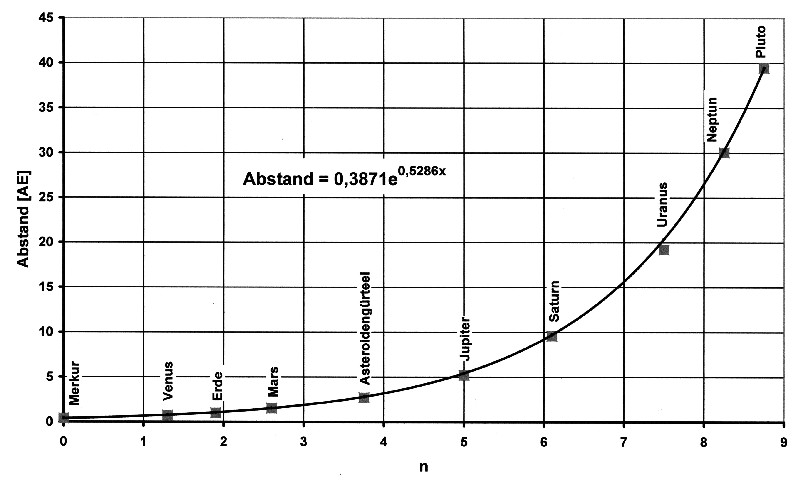
Abbildung 8.2.6 – Planetenbahnen als e-Funktion
| Es
existiert noch die Möglichkeit für die
Nummerierungswerte eine bessere Anpassung zu erhalten.
Ausgehend von der bisherigen Linearisierung lassen sich
genaue Nummern nämlich berechnen, genau so wie es schon
bei den Sonnenschalen zu sehen war. In der folgenden Tabelle sind sowohl die berechneten Nummerierungswerte als auch die angenäherten Nummern und die Ausgangsnummern zu sehen. |
| Planet | Nr | Abstand | Nr | Nr |
| alt | [AE] | genähert | berechnet | |
Merkur |
0 |
0,3871 |
0 |
0 |
Venus |
1 |
0,723 |
1,3 |
1,182 |
Erde |
2 |
1 |
1,9 |
1,796 |
Mars |
3 |
1,524 |
2,6 |
2,593 |
Asteroidengürtel |
4 |
2,7 |
3,75 |
3,675 |
Jupiter |
5 |
5,203 |
5 |
4,916 |
Saturn |
6 |
9,582 |
6,1 |
6,071 |
Uranus |
7 |
19,201 |
7,5 |
7,386 |
Neptun |
8 |
30,047 |
8,25 |
8,233 |
Pluto |
9 |
39,482 |
8,75 |
8,750 |
Die genauere Funktion für die Planetenbahnen ist in der folgenden Abbildung 8.2.7 dargestellt.
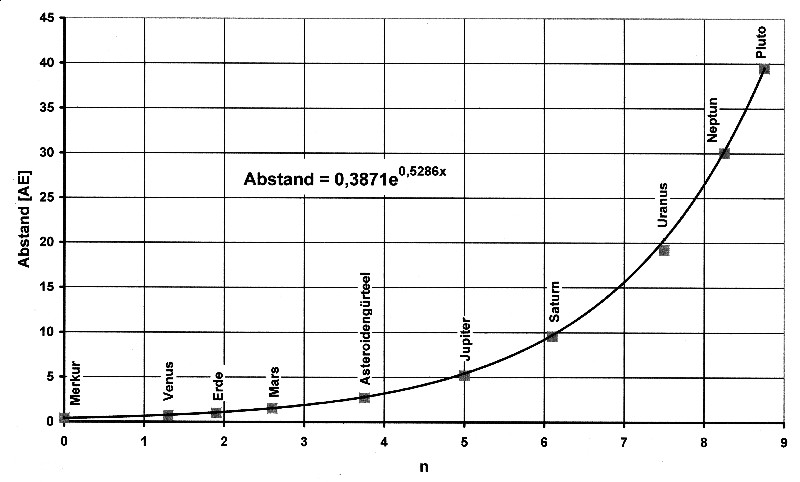
Abbildung 8.2.7 – Planetenbahnen
| Zwischen Bahnradien und Umlaufzeiten existiert ein mathematisches Verhältnis für die Planeten, dass es gestattet auch die Umlaufzeiten als e-Funktion darzustellen. |
| Zwischen Bahnradien und Umlaufzeiten der Planeten existiert ein mathematisches Verhältnis, das Johannes Kepler (*27.Dez. 1571jul - †15.Nov. 1630greg) ein deutscher Naturphilosoph, Mathematiker, Astronom Anfang des 17.ten Jahrhunderts entdeckte. Es gestattet auch die Umlaufzeiten als e-Funktion darzustellen. |
| Es gilt allgemein: |
|
| Für den Merkur (T0, r0) gilt dann ebenso: |
|
Durch Umstellen ergibt sich die Gleichung für die Umlaufzeiten der Planeten:
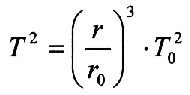
| Es gilt: r/r0 = eax und x = berechnete Nummerierung |
| Einsetzen aller Größen liefert: |
|
|
US-Astronomen sind 2005 auf einen neuen Planeten hinter Pluto gestoßen, der aus Eis und
Gestein besteht. Es ist der zehnte Planet unseres Sonnensystems. Aufgrund des bestehenden Modells lässt sich der Abstand zur Sonne ermitteln. Für die Planetenbahnen gilt: Abstand = 0,3871 · e0,52856x[AE] Es gilt: x = 10. Aufgrund der bisherigen Werte wird eine Toleranz von ±0,25 angenommen. Damit ergibt sich der Bereich für den Abstand des zehnten Planeten zwischen 67 AE und 87 AE. Der genaue Wert für x=10 ergibt sich zu 76,44 AE. |

|
284
Seiten, davon 44 in Farbe 220 Bilder 57 Tabellen Herstellung
und Verlag: ISBN 978-3-7494-8112-5 Ladenpreis: 17,50 Euro |